
如圖,已知點 在圓柱
在圓柱 的底面圓
的底面圓 上,
上, 為圓
為圓 的直徑,圓柱
的直徑,圓柱 的表面積為
的表面積為 ,
, ,
, 。
。
(1)求三棱錐 的體積。
的體積。
(2)求異面直線 與
與 所成角的余弦值;
所成角的余弦值;

(1)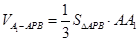
 ;(2)
;(2)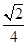 .
.
【解析】本試題主要是考查了棱錐的體積和異面直線的所成角的余弦值的求解的綜合運用。
(1)因為根據已知條件中圓柱的表面積和長度和角度問題可知得到錐體的底面的面積的求解以及最終的體積的表示。
(2)因為異面直線的所成的角一般通過平移得到,那么平移后的夾角為所求的異面直線的角。
解:
(1)由題意 ,解得
,解得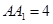 . -------------------2分
. -------------------2分
在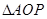 中,
中,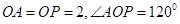 ,所以
,所以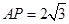 -------------------3分
-------------------3分
在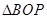 中,
中,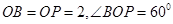 ,所以
,所以 -------------------4分
-------------------4分
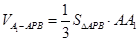 -------------------5分
-------------------5分
 -------------------6分
-------------------6分
(2)取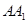 中點
中點 ,連接
,連接 ,
,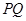 ,則
,則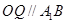 ,
,
得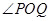 或它的補角為異面直線
或它的補角為異面直線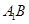 與
與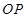 所成的角. -------------------8分
所成的角. -------------------8分
又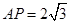 ,
,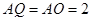 ,得
,得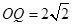 ,
,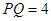 , -------------------10分
, -------------------10分
由余弦定理得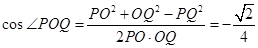 ,
,
所以異面直線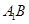 與
與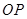 所成角的余弦值是
所成角的余弦值是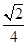 .-------------------12分
.-------------------12分


科目:高中數學 來源: 題型:
(本題滿分14分)第(1)小題滿分6分,第(2)小題滿分8分。
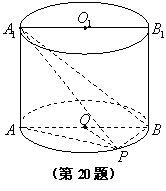 如圖,已知點
如圖,已知點![]() 在圓柱
在圓柱![]() 的底面圓
的底面圓![]() 上,
上,![]() 為圓
為圓![]() 的直徑,圓柱
的直徑,圓柱![]() 的表面積為
的表面積為![]() ,
,![]() ,
,![]() 。
。
(1)求三棱錐![]() 的體積。
的體積。
(2)求異面直線![]() 與
與![]() 所成角的大小;
所成角的大小;
(結果用反三角函數值表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
|
(本題滿分14分)第(1)小題滿分7分,第(2)小題滿分7分。
求異面直線與所成角的大小; (結果用反三角函數值表示) (2)求點到平面的距離。 查看答案和解析>> 科目:高中數學 來源: 題型: (本題滿分14分)第(1)小題滿分6分,第(2)小題滿分8分。
(1)求三棱錐 (2)求異面直線 (結果用反三角函數值表示) 查看答案和解析>> 科目:高中數學 來源: 題型: 上海市徐匯區2011屆高三下學期學習能力診斷卷(數學理).doc | | |
|