
已知曲線 .
.
(1)若曲線C在點 處的切線為
處的切線為 ,求實數
,求實數 和
和 的值;
的值;
(2)對任意實數 ,曲線
,曲線 總在直線
總在直線 :
: 的上方,求實數
的上方,求實數 的取值范圍.
的取值范圍.
(1)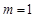 ,
, ,(2)
,(2)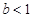 .
.
解析試題分析:(1)根據導數幾何意義,所以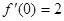 .因為
.因為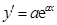 ,所以
,所以 .因為
.因為 過點
過點 ,所以
,所以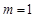 ,(2)由題意得:不等式
,(2)由題意得:不等式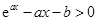 恒成立,恒成立問題一般轉化為最值問題.一是分類討論求函數
恒成立,恒成立問題一般轉化為最值問題.一是分類討論求函數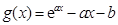 最小值,二是變量分離為
最小值,二是變量分離為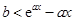 恒成立,求函數
恒成立,求函數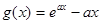 最小值.兩種方法都是
最小值.兩種方法都是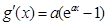 ,然后對實數a進行討論,當
,然后對實數a進行討論,當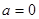 時,
時,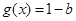 ,所以
,所以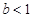 .當
.當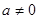 時,由
時,由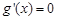 得
得 ,不論
,不論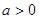 還是
還是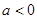 ,
,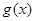 都是先減后增,即
都是先減后增,即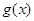 的最小值為
的最小值為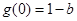 ,所以
,所以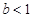 .
.
試題解析:解
(1)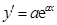 , 2分
, 2分
因為曲線C在點(0,1)處的切線為L: ,
,
所以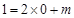 且
且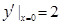 . 4分
. 4分
解得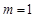 ,
, -5分
-5分
(2)法1:
對于任意實數a,曲線C總在直線的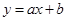 的上方,等價于
的上方,等價于
?x,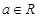 ,都有
,都有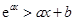 ,
,
即?x,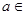 R,
R,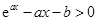 恒成立, 6分
恒成立, 6分
令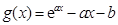 , 7分
, 7分
①若a=0,則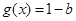 ,
,
所以實數b的取值范圍是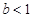 ; 8分
; 8分
②若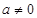 ,
,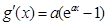 ,
,
由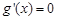 得
得 , 9分
, 9分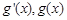 的情況如下:
的情況如下: