【答案】
分析:利用等體積,計(jì)算B
1到平面EFG距離,再利用正弦函數(shù),可求B
1F 與面GEF成角的正弦值.
解答: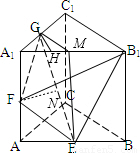
解:設(shè)正三棱柱的,取A
1B
1中點(diǎn)M,連接EM,則EM∥AA
1,EM⊥平面ABC,連接GM
∵G為A
1C
1的中點(diǎn),棱長(zhǎng)為
∴GM=

B
1C
1=1,A
1G═A
1F=1,F(xiàn)G=
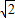
,F(xiàn)E=
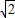
,GE=
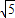
在平面EFG上作FN⊥GE,則∵△GFE是等腰三角形,∴FN=
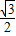
,
∴S
△GEF=

GE×FN=
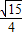
,
S
△EFB1=S
正方形ABB1A1-S
△A1B1F-S
△BB1E-S
△AFE=

,
作GH⊥A
1B
1,GH=
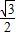
,
∴V
三棱錐G-FEB1=

S
△EFB1×GH=
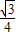
,
設(shè)B
1到平面EFG距離為h,則V
三棱錐B1-EFG=

S
△GEF=
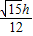
,
∵V
三棱錐G-FEB1=V
三棱錐B1-EFG,
∴
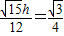
,
∴h=
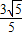
設(shè)B
1F與平面GEF成角為θ,
∵B
1F=
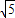
∴sinθ=
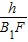
=
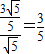
∴B
1F與面GEF所成的角的正弦值為

.
故選A.
點(diǎn)評(píng):本題考查線面角,考查三棱錐的體積計(jì)算,考查轉(zhuǎn)化思想,解題的關(guān)鍵是利用等體積計(jì)算點(diǎn)到面的距離.






 解:設(shè)正三棱柱的,取A1B1中點(diǎn)M,連接EM,則EM∥AA1,EM⊥平面ABC,連接GM
解:設(shè)正三棱柱的,取A1B1中點(diǎn)M,連接EM,則EM∥AA1,EM⊥平面ABC,連接GM B1C1=1,A1G═A1F=1,F(xiàn)G=
B1C1=1,A1G═A1F=1,F(xiàn)G=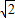 ,F(xiàn)E=
,F(xiàn)E=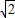 ,GE=
,GE=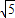
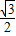 ,
, GE×FN=
GE×FN=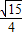 ,
, ,
,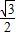 ,
, S△EFB1×GH=
S△EFB1×GH=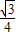 ,
, S△GEF=
S△GEF=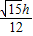 ,
,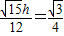 ,
,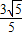
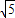
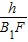 =
=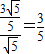
 .
.

 名校課堂系列答案
名校課堂系列答案
 如圖:在正三棱柱ABC-A1 B1 C1中,AB=
如圖:在正三棱柱ABC-A1 B1 C1中,AB= 如圖在 正三棱柱ABC-A1 B1 C1中,底面邊長(zhǎng)為
如圖在 正三棱柱ABC-A1 B1 C1中,底面邊長(zhǎng)為 如圖,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中點(diǎn),點(diǎn)N在AA1上,AN=
如圖,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中點(diǎn),點(diǎn)N在AA1上,AN= 如圖:在正三棱柱ABC-A1 B1 C1中,AB=
如圖:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F(xiàn)分別是BB1,CC1上的點(diǎn)且BE=a,CF=2a.
=a,E,F(xiàn)分別是BB1,CC1上的點(diǎn)且BE=a,CF=2a. =a,E,F(xiàn)分別是BB1,CC1上的點(diǎn)且BE=a,CF=2a.
=a,E,F(xiàn)分別是BB1,CC1上的點(diǎn)且BE=a,CF=2a.