【題目】我國古代數學家劉徽是公元三世紀世界上最杰出的數學家，他在《九章算術圓田術》注中，用割圓術證明了圓面積的精確公式，并給出了計算圓周率的科學方法.所謂“割圓術”，即通過圓內接正多邊形細割圓，并使正多邊形的周長無限接近圓的周長，進而來求得較為精確的圓周率（圓周率指圓周長與該圓直徑的比率）.劉徽計算圓周率是從正六邊形開始的，易知圓的內接正六邊形可分為六個全等的正三角形，每個三角形的邊長均為圓的半徑
，此時圓內接正六邊形的周長為
，此時若將圓內接正六邊形的周長等同于圓的周長，可得圓周率為3，當用正二十四邊形內接于圓時，按照上述算法，可得圓周率為__________．（參考數據： 
）
口算心算速算應用題系列答案
同步拓展閱讀系列答案科目：高中數學 來源： 題型：
【題目】（本小題滿分13分）
如圖5，已知點
是圓心為
半徑為1的半圓弧上從點
數起的第一個三等分點，
是直徑，
，
平面
，點
是
的中點.
（1）求二面角
的余弦值.
（2）求點
到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓G：
,過點A（0，5），B（﹣8，﹣3），C、D在該橢圓上，直線CD過原點O，且在線段AB的右下側．
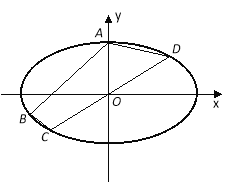
（1）求橢圓G的方程；
（2）求四邊形ABCD 的面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知隨機變量
的取值為不大于
的非負整數值，它的分布列為：
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中
（
）滿足： 
，且
．
定義由
生成的函數
，令
．
（I）若由
生成的函數
，求
的值；
（II）求證：隨機變量
的數學期望
， 
的方差
；
（
）
（Ⅲ）現投擲一枚骰子兩次，隨機變量
表示兩次擲出的點數之和，此時由
生成的函數記為
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數
的圖象形如漢字“囧”，故稱其為“囧函數”．
下列命題：
①“囧函數”的值域為
；
②“囧函數”在
上單調遞增；
③“囧函數”的圖象關于
軸對稱；
④“囧函數”有兩個零點；
⑤“囧函數”的圖象與直線
至少有一個交點．其中正確命題的個數為（ ）
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現有4個人參加某娛樂活動，該活動有甲、乙兩個游戲可供參加者選擇，為增加趣味性，約定：每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲，擲出點數為1或2的人去參加甲游戲，擲出點數大于2的人去參加乙游戲．
（1） 求出4個人中恰有2個人去 參加甲游戲的概率；
（2）求這4個人中去參加甲游戲人數大于去參加乙游戲的人數的概率；
（3）用
分別表示這4個人中去參加甲、乙游戲的人數，記
,求隨機變量
的分布列與數學期望
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點．研究表明：“活水圍網”養魚時，某種魚在一定的條件下，每尾魚的平均生長速度
（單位：千克/年）是養殖密度
（單位：尾/立方米）的函數．當不超過4（尾/立方米）時，的值為
（千克/年）；當
時，
是
的一次函數；當達到
（尾/立方米）時，因缺氧等原因，的值為
（千克/年）．
（1）當
時，求函數
的表達式；
（2）當養殖密度為多大時，魚的年生長量（單位：千克/立方米）
可以達到最大，并求出最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
