
【題目】已知二次函數(shù)![]() 的圖象過(guò)點(diǎn)
的圖象過(guò)點(diǎn)![]() ,且不等式
,且不等式![]() 的解集為
的解集為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上有最小值
上有最小值![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(3)設(shè)![]() ,若當(dāng)
,若當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的圖象恒在
的圖象恒在![]() 圖象的上方,求實(shí)數(shù)m的取值范圍.
圖象的上方,求實(shí)數(shù)m的取值范圍.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3) ![]() .
.
【解析】
(1)通過(guò)![]() ,求出
,求出![]() ,利用1和3是方程
,利用1和3是方程![]() 的兩根,結(jié)合韋達(dá)定理,求解函數(shù)的解析式.(2)
的兩根,結(jié)合韋達(dá)定理,求解函數(shù)的解析式.(2)![]() ,
,![]() ,
,![]() .對(duì)稱(chēng)軸為
.對(duì)稱(chēng)軸為![]() ,分當(dāng)
,分當(dāng)![]() 時(shí)、當(dāng)
時(shí)、當(dāng)![]() 時(shí)、當(dāng)
時(shí)、當(dāng)![]() 時(shí)情況討論函數(shù)的單調(diào)性求解函數(shù)的最值即可.
時(shí)情況討論函數(shù)的單調(diào)性求解函數(shù)的最值即可.
(3)當(dāng)![]() ,
,![]() 時(shí),
時(shí),![]() 恒成立.推出
恒成立.推出![]() ,
,![]() ,
,![]() .構(gòu)造函數(shù)通過(guò)換元法以及函數(shù)的單調(diào)性求解函數(shù)的最值,轉(zhuǎn)化求解實(shí)數(shù)
.構(gòu)造函數(shù)通過(guò)換元法以及函數(shù)的單調(diào)性求解函數(shù)的最值,轉(zhuǎn)化求解實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(1)由![]() ,得
,得![]() ,
,
又1和3是方程![]() 的兩根,
的兩根,
所以![]() ,
,![]() .
.
解得![]() ,
,![]() ,
,
因此![]() .
.
(2)![]() ,
,![]() ,
,![]() .
.
對(duì)稱(chēng)軸為![]() ,分情況討論:
,分情況討論:
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() ,
,![]() 上為增函數(shù),
上為增函數(shù),![]() ,
,
解得![]() ,符合題意;
,符合題意;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() ,
,![]() 上為減函數(shù),
上為減函數(shù),![]() 在
在![]() ,
,![]() 上為增函數(shù),
上為增函數(shù),![]() ,
,
解得![]() ,其中
,其中![]() 舍去;
舍去;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() ,
,![]() 上為減函數(shù),
上為減函數(shù),![]() (2)
(2)![]() ,
,
解得![]() ,不符合題意.
,不符合題意.
綜上可得,![]() 或
或![]() .
.
(3)由題意,當(dāng)![]() ,
,![]() 時(shí),
時(shí),![]() 恒成立.
恒成立.
即![]() ,
,![]() ,
,![]() .
.
設(shè)![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
令![]() ,于是上述函數(shù)轉(zhuǎn)化為
,于是上述函數(shù)轉(zhuǎn)化為![]() ,
,
因?yàn)?/span>![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
又![]() 在
在![]() ,
,![]() 上單調(diào)遞減,所以當(dāng)
上單調(diào)遞減,所以當(dāng)![]() 時(shí),
時(shí),![]() ,
,
于是實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是某市2017年3月1日至16日的空氣質(zhì)量指數(shù)趨勢(shì)圖,空氣質(zhì)量指數(shù)![]() 小于
小于![]() 表示空氣質(zhì)量?jī)?yōu)良,空氣質(zhì)量指數(shù)大于
表示空氣質(zhì)量?jī)?yōu)良,空氣質(zhì)量指數(shù)大于![]() 表示空氣重度污染,某人隨機(jī)選擇3月1日至3月14日中的某一天到達(dá)該市.
表示空氣重度污染,某人隨機(jī)選擇3月1日至3月14日中的某一天到達(dá)該市.
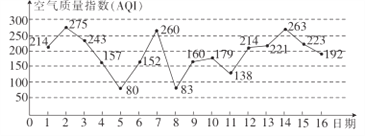
(1)若該人到達(dá)后停留![]() 天(到達(dá)當(dāng)日算1天),求此人停留期間空氣質(zhì)量都是重度污染的概率;
天(到達(dá)當(dāng)日算1天),求此人停留期間空氣質(zhì)量都是重度污染的概率;
(2)若該人到達(dá)后停留3天(到達(dá)當(dāng)日算1天〉,設(shè)![]() 是此人停留期間空氣重度污染的天數(shù),求
是此人停留期間空氣重度污染的天數(shù),求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f(x)的定義域?yàn)?/span>R,并且圖象關(guān)于y軸對(duì)稱(chēng),當(dāng)x≤-1時(shí),y=f(x)的圖象是經(jīng)過(guò)點(diǎn)(-2,0)與(-1,1)的射線,又在y=f(x)的圖象中有一部分是頂點(diǎn)在(0,2),且經(jīng)過(guò)點(diǎn)(1,1)的一段拋物線.
(1)試求出函數(shù)f(x)的表達(dá)式,作出其圖象;
(2)根據(jù)圖象說(shuō)出函數(shù)的單調(diào)區(qū)間,以及在每一個(gè)單調(diào)區(qū)間上函數(shù)是增函數(shù)還是減函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() 的圖象過(guò)點(diǎn)
的圖象過(guò)點(diǎn)![]() ,且不等式
,且不等式![]() 的解集為
的解集為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上有最小值
上有最小值![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的值;
的值;
(3)設(shè)![]() ,若當(dāng)
,若當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的圖象恒在
的圖象恒在![]() 圖象的上方,求實(shí)數(shù)m的取值范圍.
圖象的上方,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)P是拋物線y2=﹣8x上一點(diǎn),設(shè)P到此拋物線準(zhǔn)線的距離是d1,到直線x+y﹣10=0的距離是d2,則dl+d2的最小值是__.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)A(-2,0),B(2,0),曲線C上的動(dòng)點(diǎn)P滿足![]() .
.
(1)求曲線C的方程;
(2)若過(guò)定點(diǎn)M(0,-2)的直線l與曲線C有公共點(diǎn),求直線l的斜率k的取值范圍;
(3)若動(dòng)點(diǎn)Q(x,y)在曲線C上,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),解不等式
時(shí),解不等式![]() ;
;
(2)若關(guān)于![]() 的方程
的方程![]() 的解集中恰有一個(gè)元素,求
的解集中恰有一個(gè)元素,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,若對(duì)任意
,若對(duì)任意![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值與最小值的差不超過(guò)1,求
上的最大值與最小值的差不超過(guò)1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線在點(diǎn)![]() 處的切線經(jīng)過(guò)
處的切線經(jīng)過(guò)![]() ,求
,求![]() 的值;
的值;
(2)若關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(1)若![]() 是函數(shù)的極值點(diǎn),求
是函數(shù)的極值點(diǎn),求![]() 的值及函數(shù)
的值及函數(shù)![]() 的極值;
的極值;
(2)討論函數(shù)的單調(diào)性.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com