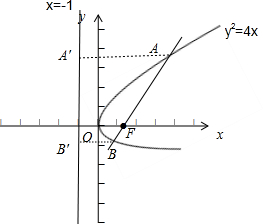分析:(1)依題意,可求得拋物線y
2=4x的焦點F(1,0),設出直線AB的方程為y=k(x-1),將直線AB的方程與拋物線方程y
2=4x聯立,利用|AB|=
即可求得k,從而可得直線AB的方程;
(2)由(1)可知直線AB的方程,利用直線AB的方程與拋物線方程y
2=4x聯立得到的關于x的一元二次方程可求得A,B兩點的坐標,設出△AOB外接圓方程為x
2+y
2+Dx+Ey+F=0,
將A,O,B三點的坐標代入,即可求得D,E,F.
解答:解:(1)∵y
2=4x的焦點F(1,0),
依題意,設直線AB的方程為y=k(x-1),因為|AB|=
,
由拋物線的定義可得:|AB|=|AA′|+|BB′|=x
1+1+x
2+1=
,
∴x
1+x
2=
.
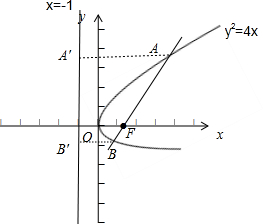
由
得:k
2x
2-(2k
2+4)x+k
2=0,
∴x
1+x
2=
=
,
∴k
2=
,又k>0,
∴k=
.
∴直線AB的方程為:y=
(x-1).
(2)將k
2=
代入k
2x
2-(2k
2+4)x+k
2=0得:4x
2-17x+4=0,
∴x=
或x=4,即x
1=4,x
2=
,將x
1,x
2分別代入直線AB的方程y=
(x-1)得:y
1=4,y
2=-1.
∴A(4,4),B(
,-1).
設△AOB外接圓方程為x
2+y
2+Dx+Ey+F=0,
則:
,解得
.
故△AOB外接圓方程為x
2+y
2-
x-
y=0.
點評:本題考查拋物線的簡單性質,考查直線與圓錐曲線的關系,考查方程思想與等價轉換思想的綜合運用,考查推理與運算能力,屬于難題.