
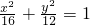 ,雙曲線C2與C1具有相同的焦點,且離心率互為倒數.
,雙曲線C2與C1具有相同的焦點,且離心率互為倒數. (a>0,b>0)
(a>0,b>0) ,焦點為F(±2,0),
,焦點為F(±2,0),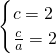 ,
,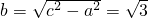 .
.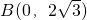 ,雙曲線C2的頂點為M(±1,0),橢圓C1與雙曲線C2的交點為N(±2,±3),
,雙曲線C2的頂點為M(±1,0),橢圓C1與雙曲線C2的交點為N(±2,±3),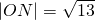 .
.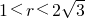 或
或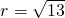 或r>4.
或r>4. ,
,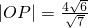 ,
,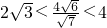 ,且
,且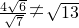 ,
,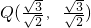 ,
,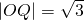 ,
,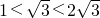 ,符合要求,
,符合要求,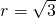 時,交點有且僅有四個,順次連接這四個交點所得到的四邊形是正方形.
時,交點有且僅有四個,順次連接這四個交點所得到的四邊形是正方形. (a>0,b>0),由雙曲線C2與C1具有相同的焦點,且離心率互為倒數,知
(a>0,b>0),由雙曲線C2與C1具有相同的焦點,且離心率互為倒數,知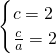 ,由此可求出雙曲線C2的方程.
,由此可求出雙曲線C2的方程.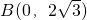 ,雙曲線C2的頂點為M(±1,0),橢圓C1與雙曲線C2的交點為N(±2,±3),
,雙曲線C2的頂點為M(±1,0),橢圓C1與雙曲線C2的交點為N(±2,±3),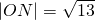 .所以圓C與兩曲線C1、C2有且僅有四個交點,再運用曲線的對稱性將問題轉化從而簡化計算.
.所以圓C與兩曲線C1、C2有且僅有四個交點,再運用曲線的對稱性將問題轉化從而簡化計算.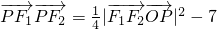 ,則動點軌跡也是曲線C2.
,則動點軌跡也是曲線C2. 

科目:高中數學 來源:2012-2013學年貴州省六校聯盟高三(上)第一次聯考數學試卷(文科)(解析版) 題型:選擇題
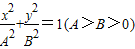 和雙曲線C2:
和雙曲線C2: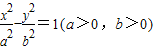 有相同的焦點F1、F2,2c是它們的共同焦距,且它們的離心率互為倒數,P是它們在第一象限的交點,當cos∠F1PF2=60°時,下列結論中正確的是( )
有相同的焦點F1、F2,2c是它們的共同焦距,且它們的離心率互為倒數,P是它們在第一象限的交點,當cos∠F1PF2=60°時,下列結論中正確的是( )查看答案和解析>>
科目:高中數學 來源:2008-2009學年河北省衡水市中學高二(上)第二次調研數學試卷(解析版) 題型:解答題
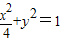 ,雙曲線C2:
,雙曲線C2: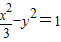 .若直線
.若直線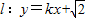 與橢圓C1、雙曲線C2都恒有兩個不同的交點,且l與C2的兩交點A、B滿足
與橢圓C1、雙曲線C2都恒有兩個不同的交點,且l與C2的兩交點A、B滿足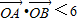 (其中O為原點),求k的取值范圍.
(其中O為原點),求k的取值范圍.查看答案和解析>>
科目:高中數學 來源:2010年廣東省江門市高考數學后階段備考指導和猜題試卷(解析版) 題型:解答題
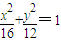 ,雙曲線C2與C1具有相同的焦點,且離心率互為倒數.
,雙曲線C2與C1具有相同的焦點,且離心率互為倒數.查看答案和解析>>
科目:高中數學 來源:2011年高考數學綜合復習試卷(2)(解析版) 題型:解答題
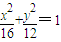 ,雙曲線C2與C1具有相同的焦點,且離心率互為倒數.
,雙曲線C2與C1具有相同的焦點,且離心率互為倒數.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com