
【題目】設函數![]() .
.
(1)求函數![]() 的單調遞減區間;
的單調遞減區間;
(2)若![]() ,對于給定實數
,對于給定實數![]() ,總存在實數
,總存在實數![]() ,使得關于
,使得關于![]() 的方程
的方程![]() 恰有3個不同的實數根.
恰有3個不同的實數根.
(i)求實數![]() 的取值范圍;
的取值范圍;
(ii)記![]() ,求證:
,求證:![]() .
.
【答案】(1)單調遞減區間是![]() ,
,![]() ;(2)(i)
;(2)(i)![]() ;(ii)證明見詳解.
;(ii)證明見詳解.
【解析】
(1)當![]() ,
,![]() ,當
,當![]() 時,可知
時,可知![]() ,此時
,此時![]() 無單調遞減區間;當
無單調遞減區間;當![]() 時,令
時,令![]() ,可得
,可得![]() ,再根據
,再根據![]() 為偶函數,即可求出函數
為偶函數,即可求出函數 ![]() 的單調遞減區間;
的單調遞減區間;
(2)(i)![]()
![]() ,令
,令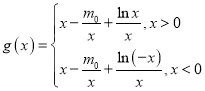 ,則
,則![]() ,令
,令![]() ,利用導數可得
,利用導數可得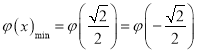 ;再分別對
;再分別對![]() 和
和![]() ,兩種情況分類討論,根據函數的單調性和奇偶性以及對稱性進行分析,即可求出結果;
,兩種情況分類討論,根據函數的單調性和奇偶性以及對稱性進行分析,即可求出結果;
(ii)由![]() 的四個根為
的四個根為![]() ,
,![]() ,
,![]() ,
,![]() ,不妨設
,不妨設![]() ,由于
,由于![]() 為偶函數,則
為偶函數,則![]() ,
, 化簡整理可得
化簡整理可得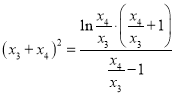 ,令
,令![]() ,
,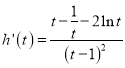 ,令
,令![]() ,根據導數在函數單調性和最值的應用,即可求證結果.
,根據導數在函數單調性和最值的應用,即可求證結果.
(1)當![]() ,
,![]() ,當
,當![]() ,
,![]() ;當
;當![]() ,
,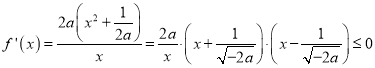 ,∴
,∴![]() .
.
又![]() 為偶函數,∴當
為偶函數,∴當![]() 時,
時,![]() 的單調遞減區間是
的單調遞減區間是![]() ,
,![]() ,
,
當![]() 時,
時,![]() 無單調遞減區間.
無單調遞減區間.
(2)(i)![]()
 ,令
,令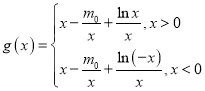 ,
,
則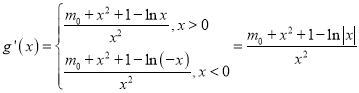 ,
,
令![]() ,
,![]() ,
,
∴![]() 在
在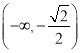 遞減,
遞減,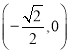 遞增,
遞增,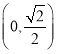 遞減,
遞減,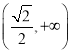 遞增.
遞增.
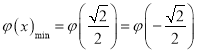 .
.
①當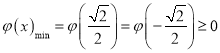 時,可得
時,可得![]() ,此時
,此時![]() ,所以
,所以![]() 在
在![]() 遞減,在
遞減,在![]() 遞增,則
遞增,則![]() 至多2個零點,不符合題意.
至多2個零點,不符合題意.
②當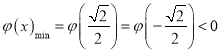 ,則
,則![]() 有4個不同實根,即
有4個不同實根,即![]() 時,
時,![]() 有2個不同實根,此時
有2個不同實根,此時![]() .
.
其中![]() ,
,![]() (極大),
(極大),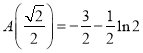 ,設
,設![]() 的4個實根為
的4個實根為![]() ,則
,則![]() 極大,
極大,![]() 極小,
極小,![]() 極大,
極大,![]() 極小,由于
極小,由于![]() 為奇函數,所以極值關于原點對稱,
為奇函數,所以極值關于原點對稱,![]() ,
,
![]() ,∴
,∴![]() ,當
,當![]() 時
時![]() 有3個零點.
有3個零點.
(ii)由![]() 的四個根為
的四個根為![]() ,
,![]() ,
,![]() ,
,![]() ,不妨設
,不妨設![]() ,由于
,由于![]() 為偶函數,則
為偶函數,則![]() ,
,
![]() ,
,
∴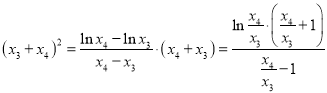 ,
,
令![]() ,
,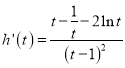 ,
,
令![]() ,
,![]() ,所以
,所以![]() 單調遞增,
單調遞增,
![]() ,所以
,所以![]() ,
,![]() 單調遞增,則
單調遞增,則![]() ,
,
所以![]() ,
,![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱,旨在積極發展我國與沿線國家經濟合作關系,共同打造政治互信、經濟融合、文化包容的命運共同體.自2013年以來,“一帶一路”建設成果顯著.下圖是2013-2017年,我國對“一帶一路”沿線國家進出口情況統計圖.下列描述錯誤的是( )
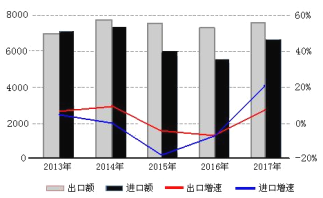
A.這五年,2013年出口額最少
B.這五年,出口總額比進口總額多
C.這五年,出口增速前四年逐年下降
D.這五年,2017年進口增速最快
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線x2=2py(p>0)的焦點為F(0,1),過F的兩條動直線AB,CD與拋物線交出A、B、C、D四點,直線AB,CD的斜率存在且分別是k1(k1>0),k2.
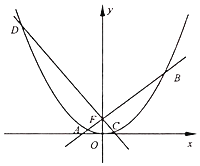
(Ⅰ)若直線BD過點(0,3),求直線AC與y軸的交點坐標
(Ⅱ)若k1﹣k2=2,求四邊形ACBD面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是反映空氣質量狀況的指數,AQI指數值越小,表明空氣質量越好,其對應關系如下表:
AQI指數值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數變化趨勢:

下列敘述錯誤的是
A. 這20天中AQI指數值的中位數略高于100
B. 這20天中的中度污染及以上的天數占![]()
C. 該市10月的前半個月的空氣質量越來越好
D. 總體來說,該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某區在2019年教師招聘考試中,參加![]() 、
、![]() 、
、![]() 、
、![]() 四個崗位的應聘人數、錄用人數和錄用比例(精確到1%)如下:
四個崗位的應聘人數、錄用人數和錄用比例(精確到1%)如下:
崗位 | 男性應聘人數 | 男性錄用人數 | 男性錄用比例 | 女性應聘人數 | 女性錄用人數 | 女性錄用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
總計 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)從表中所有應聘人員中隨機抽取1人,試估計此人被錄用的概率;
(2)將應聘![]() 崗位的男性教師記為
崗位的男性教師記為![]() ,女性教師記為
,女性教師記為![]() ,現從應聘
,現從應聘![]() 崗位的6人中隨機抽取2人.
崗位的6人中隨機抽取2人.
(i)試用所給字母列舉出所有可能的抽取結果;
(ii)設![]() 為事件“抽取的2人性別不同”,求事件
為事件“抽取的2人性別不同”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com