
如圖,已知⊙O的半徑為1,MN是⊙O的直徑,過M點(diǎn)作⊙O的切線AM,C是AM的中點(diǎn),AN交⊙O于B點(diǎn),若四邊形BCON是平行四邊形;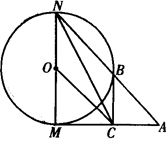
(Ⅰ)求AM的長;
(Ⅱ)求sin∠ANC.
(Ⅰ)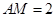 ;(Ⅱ)
;(Ⅱ) .
.
解析試題分析:(Ⅰ)先證得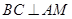 ,
, ,即可得
,即可得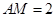 ;(Ⅱ)作
;(Ⅱ)作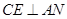 ,得
,得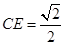 ,再在
,再在 中求解sin∠ANC.
中求解sin∠ANC.
試題解析:(Ⅰ)連接 ,則
,則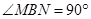 ,
,
因?yàn)樗倪呅?img src="http://thumb.zyjl.cn/pic5/tikupic/5c/8/1ub9z2.png" style="vertical-align:middle;" />是平行四邊形,所以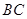 ∥
∥ ,
,
因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/a8/a/mwsjo.png" style="vertical-align:middle;" />是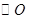 的切線,所以
的切線,所以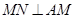 ,可得
,可得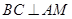 ,
,
又因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/ec/d/1hlox2.png" style="vertical-align:middle;" />是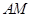 的中點(diǎn),所以
的中點(diǎn),所以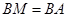 ,得
,得 ,故
,故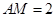 . (5分)
. (5分)
(Ⅱ)作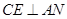 于
于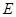 點(diǎn),則
點(diǎn),則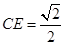 ,由(Ⅰ)可知
,由(Ⅰ)可知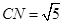 ,
,
故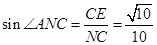 . (10分)
. (10分)
考點(diǎn):平面幾何關(guān)系證明.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖, 是⊙
是⊙ 的直徑,
的直徑, 是⊙
是⊙ 的切線,
的切線, 與
與 的延長線交于點(diǎn)
的延長線交于點(diǎn) ,
, 為切點(diǎn).若
為切點(diǎn).若 ,
, ,
, 的平分線
的平分線 與
與 和⊙
和⊙ 分別交于點(diǎn)
分別交于點(diǎn) 、
、 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
切線 與圓切于點(diǎn)
與圓切于點(diǎn) ,圓內(nèi)有一點(diǎn)
,圓內(nèi)有一點(diǎn) 滿足
滿足 ,
, 的平分線
的平分線 交圓于
交圓于 ,
, ,延長
,延長 交圓于
交圓于 ,延長
,延長 交圓于
交圓于 ,連接
,連接 .
.
(Ⅰ)證明: //
// ;
;
(Ⅱ)求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示,自⊙ 外一點(diǎn)
外一點(diǎn)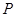 引切線與⊙
引切線與⊙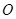 切于點(diǎn)
切于點(diǎn) ,
,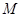 為
為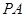 的中點(diǎn),過
的中點(diǎn),過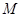 引割線交⊙
引割線交⊙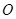 于
于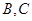 兩點(diǎn). 求證:
兩點(diǎn). 求證:
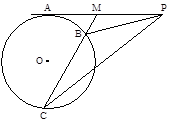
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知⊙O是 的外接圓,
的外接圓,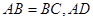 是
是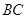 邊上的高,
邊上的高,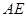 是⊙O的直徑.
是⊙O的直徑.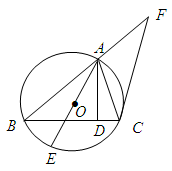
(1)求證: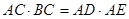 ;
;
(II)過點(diǎn)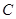 作⊙O的切線交
作⊙O的切線交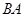 的延長線于點(diǎn)
的延長線于點(diǎn)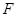 ,若
,若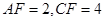 ,求
,求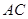 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,過圓O外一點(diǎn)P作該圓的兩條割線PAB和PCD,分別交圓O于點(diǎn)A,B,C,D弦AD和BC交于Q點(diǎn),割線PEF經(jīng)過Q點(diǎn)交圓O于點(diǎn)E、F,點(diǎn)M在EF上,且 :
:
(I)求證:PA·PB=PM·PQ.
(II)求證: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知,如圖,在平行四邊形ABCD中,延長DA到點(diǎn)E,延長BC到點(diǎn)F,使得AE=CF,連接EF,分別交AB,CD于點(diǎn)M,N,連接DM,BN.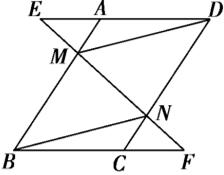
(1)求證:△AEM ≌△CFN;
(2)求證:四邊形BMDN是平行四邊形.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com