
【題目】已知![]() ,
,![]() .
.
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,若關于
時,若關于![]() 的方程
的方程![]() 存在兩個正實數根
存在兩個正實數根![]() ,證明:
,證明:![]() 且
且![]() .
.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1)求出函數的導函數,再計算出![]() ,
,![]() ,即可求出切線方程;
,即可求出切線方程;
(2)由![]() 存在兩個正實數根
存在兩個正實數根![]() ,整理得方程
,整理得方程![]() 存在兩個正實數根
存在兩個正實數根![]() .令
.令![]() 利用導數研究其單調性、最值,因為
利用導數研究其單調性、最值,因為![]() 有兩個零點,即
有兩個零點,即![]() ,得
,得![]() .
.
因為實數![]() ,
,![]() 是
是![]() 的兩個根,所以
的兩個根,所以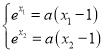 ,從而
,從而![]() .令
.令![]() ,
,![]() ,則
,則![]() ,變形整理得
,變形整理得![]() .要證
.要證![]() ,則只需證
,則只需證![]() ,即只要證
,即只要證![]() ,
,
再構造函數即可證明.
(1)解:∵ ,
,
∴![]() ,
,![]() ,
,
∴曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(2)證明:由![]() 存在兩個正實數根
存在兩個正實數根![]() ,
,
整理得方程![]() 存在兩個正實數根
存在兩個正實數根![]() .
.
由![]() ,知
,知![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減.
上單調遞減.
所以![]() .
.
因為![]() 有兩個零點,即
有兩個零點,即![]() ,得
,得![]() .
.
因為實數![]() ,
,![]() 是
是![]() 的兩個根,
的兩個根,
所以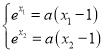 ,從而
,從而![]() .
.
令![]() ,
,![]() ,則
,則![]() ,變形整理得
,變形整理得![]() .
.
要證![]() ,則只需證
,則只需證![]() ,即只要證
,即只要證![]() ,
,
結合對數函數![]() 的圖象可知,只需要證
的圖象可知,只需要證![]() ,
,![]() 兩點連線的斜率要比
兩點連線的斜率要比![]() ,
,![]() 兩點連線的斜率小即可.
兩點連線的斜率小即可.
因為![]() ,所以只要證
,所以只要證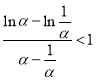 ,整理得
,整理得![]() .
.
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上單調遞減,即
上單調遞減,即![]() ,
,
所以![]() 成立,故
成立,故![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】十九大以來,某貧困地區扶貧辦積極貫徹落實國家精準扶貧的政策要求,帶領廣大農村地區人民群眾脫貧奔小康。經過不懈的奮力拼搏,新農村建設取得巨大進步,農民年收入也逐年增加。為了更好的制定2019年關于加快提升農民年收人力爭早日脫貧的工作計劃,該地扶貧辦統計了2018年![]() 位農民的年收人并制成如下頻率分布直方圖:
位農民的年收人并制成如下頻率分布直方圖:
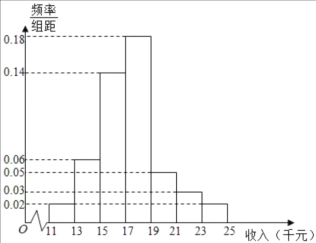
(1)根據頻率分布直方圖,估計![]() 位農民的年平均收入
位農民的年平均收入![]() (單位:千元)(同一組數據用該組數據區間的中點值表示);
(單位:千元)(同一組數據用該組數據區間的中點值表示);
(2)由頻率分布直方圖,可以認為該貧困地區農民年收入![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為年平均收入
近似為年平均收入![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,經計算得
,經計算得![]() .利用該正態分布,求:
.利用該正態分布,求:
(i)在2019年脫貧攻堅工作中,若使該地區約有占總農民人數的![]() 的農民的年收入高于扶貧辦制定的最低年收入標準,則最低年收入大約為多少千元?
的農民的年收入高于扶貧辦制定的最低年收入標準,則最低年收入大約為多少千元?
(ii)為了調研“精準扶貧,不落一人”的政策要求落實情況,扶貧辦隨機走訪了![]() 位農民。若每個農民的年收人相互獨立,問:這
位農民。若每個農民的年收人相互獨立,問:這![]() 位農民中的年收入不少于
位農民中的年收入不少于![]() 千元的人數最有可能是多少?
千元的人數最有可能是多少?
附:參考數據與公式![]()
則①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 與
與![]() 的公共點
的公共點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 且與
且與![]() 相切的直線交
相切的直線交![]() 于另一點
于另一點![]() ,過
,過![]() 且與
且與![]() 相切的直線交
相切的直線交![]() 于另一點
于另一點![]() ,記
,記![]() 為
為![]() 的面積.
的面積.
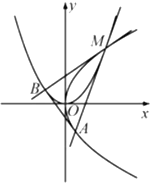
(Ⅰ)求![]() 的值(用
的值(用![]() 表示);
表示);
(Ⅱ)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
注:若直線與拋物線有且只有一個公共點,且與拋物線的對稱軸不平行也不重合,則稱該直線與拋物線相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在古裝電視劇《知否》中,甲乙兩人進行一種投壺比賽,比賽投中得分情況分“有初”“貫耳”“散射”“雙耳”“依竿”五種,其中“有初”算“兩籌”,“貫耳”算“四籌”,“散射”算“五籌”,“雙耳”算“六籌”,“依竿”算“十籌”,三場比賽得籌數最多者獲勝.假設甲投中“有初”的概率為![]() ,投中“貫耳”的概率為
,投中“貫耳”的概率為![]() ,投中“散射”的概率為
,投中“散射”的概率為![]() ,投中“雙耳”的概率為
,投中“雙耳”的概率為![]() ,投中“依竿”的概率為
,投中“依竿”的概率為![]() ,乙的投擲水平與甲相同,且甲乙投擲相互獨立.比賽第一場,兩人平局;第二場,甲投了個“貫耳”,乙投了個“雙耳”,則三場比賽結束時,甲獲勝的概率為( )
,乙的投擲水平與甲相同,且甲乙投擲相互獨立.比賽第一場,兩人平局;第二場,甲投了個“貫耳”,乙投了個“雙耳”,則三場比賽結束時,甲獲勝的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 是橢圓
是橢圓![]() 上的一個動點,且
上的一個動點,且![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 斜率為
斜率為![]() ,且
,且![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 若存在,求
若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 是邊長為2的菱形,且
是邊長為2的菱形,且![]() ,
,![]() 是矩形,
是矩形,![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 點在線段
點在線段![]() 上移動(
上移動(![]() 不與
不與![]() 重合),
重合),![]() 是
是![]() 的中點.
的中點.
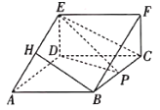
(1)當四面體![]() 的外接球的表面積為
的外接球的表面積為![]() 時,證明:
時,證明:![]() .平面
.平面![]()
(2)當四面體![]() 的體積最大時,求平面
的體積最大時,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北方的冬天戶外冰天雪地,若水管裸露在外,則管內的水就會結冰從而凍裂水管,給用戶生活帶來不便.每年冬天來臨前,工作人員就會給裸露在外的水管“保暖”:在水管外面包裹保溫帶,用一條保溫帶盤旋而上一次包裹到位.某工作人員采用四層包裹法(除水管兩端外包裹水管的保溫帶都是四層):如圖1所示是相鄰四層保溫帶的下邊緣輪廓線,相鄰兩條輪廓線的間距是帶寬的四分之一.設水管的直徑與保溫帶的寬度都為4cm.在圖2水管的側面展開圖中,此保溫帶的輪廓線與水管母線所成的角的余弦值是( )(保溫帶厚度忽略不計)
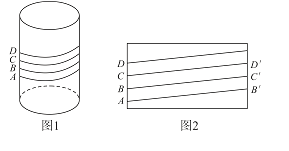
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為內角
分別為內角![]() ,
,![]() ,
,![]() 的對邊,且滿
的對邊,且滿![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中,選出兩個使
這三個條件中,選出兩個使![]() 唯一確定的條件補充在下面的問題中,并解答問題.若________,________,求
唯一確定的條件補充在下面的問題中,并解答問題.若________,________,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com