
【題目】已知四棱柱![]() 的所有棱長都為2,且
的所有棱長都為2,且![]() .
.
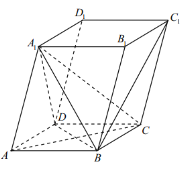
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成的角
所成的角![]() 的正弦值.
的正弦值.
科目:高中數學 來源: 題型:
【題目】已知![]() 兩點分別在
兩點分別在![]() 軸和
軸和![]() 軸上運動,且
軸上運動,且![]() ,若動點
,若動點![]() 滿足
滿足![]() .
.
(1)求出動點![]() 的軌跡
的軌跡![]() 的標準方程;
的標準方程;
(2)設動直線![]() 與曲線
與曲線![]() 有且僅有一個公共點,與圓
有且僅有一個公共點,與圓![]() 相交于兩點
相交于兩點![]() (兩點均不在坐標軸上),求直線
(兩點均不在坐標軸上),求直線![]() 的斜率之積.
的斜率之積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小軍的微信朋友圈參與了“微信運動”,他隨機選取了40位微信好友(女20人,男20人),統計其在某一天的走路步數.其中,女性好友的走路步數數據記錄如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步數情況可分為五個類別(說明:m~n表示大于等于m,小于等于n):A(0~2000步)1人,B(2001~5000步)2人,C(5001~8000步)3人,D(8001~10000步)6人,E(10001步及以上)8人.若某人一天的走路步數超過8000步被系統認定為“健康型”,否則被系統認定為“進步型”.
(1)請根據選取的樣本數據完成下面的![]() 列聯表,并根據此判斷能否有95%以上的把握認為“認定類型”與“性別”有關?
列聯表,并根據此判斷能否有95%以上的把握認為“認定類型”與“性別”有關?
健康型 | 進步型 | 總計 | |
男 | 20 | ||
女 | 20 | ||
總計 | 40 |
(2)從小軍的40位好友中該天走路步數不超過5000的中隨機抽取3人,若![]() 表示抽到的三人分別是x,y,z,試用該表示法列舉出試驗所有可能的結果.若記“恰好抽到了一位女性好友”為事件A,求事件A的概率.
表示抽到的三人分別是x,y,z,試用該表示法列舉出試驗所有可能的結果.若記“恰好抽到了一位女性好友”為事件A,求事件A的概率.
附: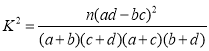 ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知定點
中,已知定點![]() ,點
,點![]() 在
在![]() 軸上運動,點
軸上運動,點![]() 在
在![]() 軸上運動,點
軸上運動,點![]() 為坐標平面內的動點,且滿足
為坐標平面內的動點,且滿足![]() ,
,![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過曲線![]() 第一象限上一點
第一象限上一點![]() (其中
(其中![]() )作切線交直線
)作切線交直線![]() 于點
于點![]() ,連結
,連結![]() 并延長交直線
并延長交直線![]() 于點
于點![]() ,求當
,求當![]() 面積取最小值時切點
面積取最小值時切點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,過點
,過點![]() 作
作![]() 的異于
的異于![]() 軸的切線
軸的切線![]() ,過點
,過點![]() 作
作![]() 的異于
的異于![]() 軸的切線
軸的切線![]() .設
.設![]() 與
與![]() 交于點
交于點![]() ,記
,記![]() 的軌跡為
的軌跡為![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知![]() ,
,![]() 在點
在點![]() 處的切線交直線
處的切線交直線![]() 于點
于點![]() ,過原點
,過原點![]() 與
與![]() 平行的直線交
平行的直線交![]() 于點
于點![]() .證明:以
.證明:以![]() 為直徑的圓截
為直徑的圓截![]() 軸的弦長為定值.
軸的弦長為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】追求人類與生存環境的和諧發展是中國特色社會主義生態文明的價值取向.為了改善空氣質量,某城市環保局隨機抽取了一年內100天的空氣質量指數(AQI)的檢測數據,結果統計如表:
AQI |
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 重度污染 |
天數 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)從空氣質量指數屬于[0,50],(50,100]的天數中任取3天,求這3天中空氣質量至少有2天為優的概率;
(2)已知某企業每天因空氣質量造成的經濟損失y(單位:元)與空氣質量指數x的關系式為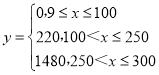 ,假設該企業所在地7月與8月每天空氣質量為優、良、輕度污染、中度污染、重度污染、嚴重污染的概率分別為
,假設該企業所在地7月與8月每天空氣質量為優、良、輕度污染、中度污染、重度污染、嚴重污染的概率分別為![]() .9月每天的空氣質量對應的概率以表中100天的空氣質量的頻率代替.
.9月每天的空氣質量對應的概率以表中100天的空氣質量的頻率代替.
(i)記該企業9月每天因空氣質量造成的經濟損失為X元,求X的分布列;
(ii)試問該企業7月、8月、9月這三個月因空氣質量造成的經濟損失總額的數學期望是否會超過2.88萬元?說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:若函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,則稱區間
,則稱區間![]() 是函數
是函數![]() 的“完美區間”,另外,定義區間
的“完美區間”,另外,定義區間![]() 的“復區間長度”為
的“復區間長度”為![]() ,已知函數
,已知函數![]() ,則( )
,則( )
A.![]() 是
是![]() 的一個“完美區間”
的一個“完美區間”
B. 是
是![]() 的一個“完美區間”
的一個“完美區間”
C.![]() 的所有“完美區間”的“復區間長度”的和為
的所有“完美區間”的“復區間長度”的和為![]()
D.![]() 的所有“完美區間”的“復區間長度”的和為
的所有“完美區間”的“復區間長度”的和為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com