分析:作出正弦函數 y=sinx的圖象,并加以觀察,并根據函數的單調性對A、B、C、D各項的結論進行推理論證,結合取特殊的a、b值檢驗,可得A、B、C都正確,而D項錯誤,由此得到答案.
解答:解:作出正弦函數 y=sinx的圖象,加以觀察得
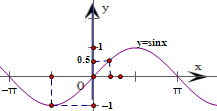
對于A,當a=
-且b=
時,函數在區間[a,b]上單調增,
可得函數的最小值為sin(
-)=-1;函數的最大值為sin
=
此時函數的值域為
[-1,],b-a的達到最小值
,故A正確;.
對于B,當a=
-且b=
時,函數在區間[a,b]上先單調遞減,
再單調遞增,
函數的最小值為sin(
-)=-1;且最大值為sin(
-)=sin
=
,
此時函數的值域為
[-1,],b-a的達到最大值
,故B正確;.
對于C,如果a=
2kπ-(k∈Z),由于sina=-
沒有達到最小值1,則b≥
2kπ+才能出現函數的最小值1,而此時函數的最大值為1而不是
,與題設矛盾
因此a不可能等于
2kπ-(k∈Z),可得C正確;
對于D,當a=
-且b=-
時,根據函數圖象可得函數的值域為
[-1,],
說明b值可能等于
2kπ-(k∈Z),故D不正確
故選:D
點評:本題給出正弦函數的幾個結論,要求找出其中的假命題,考查了正弦函數的圖象與性質等知識,屬于中檔題.




 ,給出以下四個結論:
,給出以下四個結論:

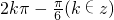
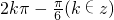 其中正確的有
其中正確的有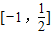 ,給出以下四個結論:
,給出以下四個結論: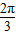
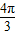
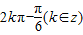
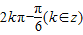 其中正確的有( )
其中正確的有( )