
【題目】若函數![]() 滿足
滿足![]() (其中
(其中![]() 且
且![]() ).
).
(1)求函數![]() 的解析式,并判斷其奇偶性和單調性;
的解析式,并判斷其奇偶性和單調性;
(2)解關于![]() 的不等式
的不等式![]() .
.
【答案】 (1) 見解析;(2) ![]() .
.
【解析】試題分析:
(1)利用換元法可得函數的解析式為![]() ,結合函數的解析式可得函數f(x)為奇函數,然后分類討論確定函數的單調性即可;
,結合函數的解析式可得函數f(x)為奇函數,然后分類討論確定函數的單調性即可;
(2)結合(1)中確定的函數的單調性和函數的奇偶性脫去f符號,得到不等式![]() ,求解不等式可得不等式的解集為
,求解不等式可得不等式的解集為![]() .
.
試題解析:
(1)令logax=t(t∈R),則x=at,
∴f(t)=![]() (at-a-t).
(at-a-t).
∴f(x)=![]() (ax-a-x)(x∈R).
(ax-a-x)(x∈R).
∵f(-x)=![]() (a-x-ax)=-
(a-x-ax)=-![]() (ax-a-x)=-f(x),∴f(x)為奇函數.
(ax-a-x)=-f(x),∴f(x)為奇函數.
當a>1時,y=ax為增函數,y=-a-x為增函數,且![]() >0,
>0,
∴f(x)為增函數.
當0<a<1時,y=ax為減函數,y=-a-x為減函數,且![]() <0,
<0,
∴f(x)為增函數.∴f(x)在R上為增函數.
(2)∵f(x)是R上的增函數且為奇函數,∴由![]() 得
得
![]() ∴
∴![]()
∴不等式![]() 的解集為
的解集為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設集合A={x|﹣1≤x≤2},B={x|x2﹣(2m+1)x+2m<0}.
(1)當m< ![]() 時,把集合B用區間表達;
時,把集合B用區間表達;
(2)若A∪B=A,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= 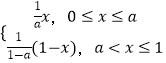 ,a為常數,且a∈(0,1).
,a為常數,且a∈(0,1).
(1)若x0滿足f(x0)=x0 , 則稱x0為f(x)的一階周期點,證明函數f(x)有且只有兩個一階周期點;
(2)若x0滿足f(f(x0))=x0 , 且f(x0)≠x0 , 則稱x0為f(x)的二階周期點,當a= ![]() 時,求函數f(x)的二階周期點.
時,求函數f(x)的二階周期點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+2alnx.
(1)若函數f(x)的圖象在(2,f(2))處的切線斜率為1,求實數a的值;
(2)求函數f(x)的單調區間;
(3)若函數 ![]() 在[1,2]上是減函數,求實數a的取值范圍.
在[1,2]上是減函數,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com