
設函數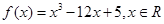 .
.
(1)求 的單調區間和極值;
的單調區間和極值;
(2)若關于 的方程
的方程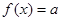 有3個不同實根,求實數a的取值范圍.
有3個不同實根,求實數a的取值范圍.
 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)=x3+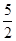 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+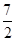 x2+ 1nx+b,(a,b為常數).
x2+ 1nx+b,(a,b為常數).
(1)若g(x)在x=l處的切線方程為y=kx-5(k為常數),求b的值;
(2)設函數f(x)的導函數為f’(x),若存在唯一的實數x0,使得f(x0)=x0與f′(x0)=0同時成立,求實數b的取值范圍;
(3)令F(x)=f(x)-g(x),若函數F(x)存在極值,且所有極值之和大于5+1n2,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設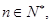 圓
圓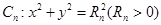 與
與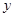 軸正半軸的交點為
軸正半軸的交點為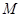 ,與曲線
,與曲線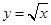 的交點為
的交點為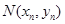 ,直線
,直線 與
與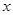 軸的交點為
軸的交點為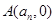 .
.
(1)用 表示
表示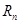 和
和
(2)若數列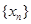 滿足
滿足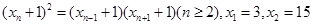
(1)求常數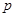 的值,使得數列
的值,使得數列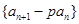 成等比數列;
成等比數列;
(2)比較 與
與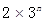 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
修建一個面積為 平方米的矩形場地的圍墻,要求在前面墻的正中間留一個寬度為2米的出入口,后面墻長度不超過20米,已知后面墻的造價為每米45元,其它墻的造價為每米180元,設后面墻長度為x米,修建此矩形場地圍墻的總費用為
平方米的矩形場地的圍墻,要求在前面墻的正中間留一個寬度為2米的出入口,后面墻長度不超過20米,已知后面墻的造價為每米45元,其它墻的造價為每米180元,設后面墻長度為x米,修建此矩形場地圍墻的總費用為 元.
元.
(1)求 的表達式;
的表達式;
(2)試確定x,使修建此矩形場地圍墻的總費用最小,并求出最小總費用.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
已知函數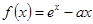 (
( 為常數)的圖象與
為常數)的圖象與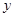 軸交于點
軸交于點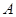 ,曲線
,曲線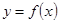 在點
在點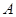 處
處
的切線斜率為-1.
(I)求 的值及函數
的值及函數 的極值;
的極值;
(II)證明:當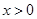 時,
時,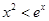 ;
;
(III)證明:對任意給定的正數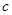 ,總存在
,總存在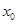 ,使得當
,使得當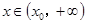 ,恒有
,恒有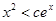 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com