
分析 (Ⅰ)利用已知條件直接列出該企業每天生產這種產品所獲得的利潤y表示為x的函數;
(Ⅱ)利用(Ⅰ)求解函數的導數,利用函數的極值以及單調性,求解函數的最值即可.
解答 (本小題滿分13分)
解:(Ⅰ)根據題意,該企業所得利潤為:y=20•[3(x-p)-p]=20(3x-4p)=60x-80p…(2分)
=60x-80(0.1125x2-3.6lnx+1)=60x-9x2+288lnx-80(4≤x≤12).…(5分)
(Ⅱ)由(Ⅰ)知:$y'=60-18x+\frac{288}{x}=\frac{{60x-18{x^2}+288}}{x}$…(6分)
=$\frac{{-6(3{x^2}-10x-48)}}{x}=\frac{-6(3x+8)(x-6)}{x}$.
令y'=0,可得x=6或$x=-\frac{8}{3}$.…(8分)
從而當4<x<6時,y'>0,函數在(4,6)上為增函數;
當6<x<12時,y'<0,函數在(6,12)上為減函數.…(9分)
所以當x=6時函數取得極大值,
即當x=6時,${y_{min}}=60×6-9×{6^2}+288ln6-80=288ln6-44$,…(12分)
所以每臺機器的日產量為6萬件時,該企業的利潤最大,
最大利潤為288ln6-44(萬元).…(13分)
點評 本題考查函數的導數的綜合應用,函數的解析式的求法,考查分析問題解決問題的能力.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:選擇題
| A. | k•360°-40°,k∈Z | B. | k•180°-40°,k∈Z | C. | k•360°+40°,k∈Z | D. | k•180°+40°,k∈Z |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
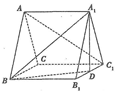 如圖,斜三棱柱ABC-A1B1C1中,AB=AC=2,平面ABC⊥平面B1BCC1,BC=BB1=2$\sqrt{3}$,∠B1BC=60°,D為B1C1的中點.
如圖,斜三棱柱ABC-A1B1C1中,AB=AC=2,平面ABC⊥平面B1BCC1,BC=BB1=2$\sqrt{3}$,∠B1BC=60°,D為B1C1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ③⑤ | C. | ②③⑤ | D. | ③④⑤ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | M∩N | B. | M∩(∁UN) | C. | (∁UM)∩N | D. | (∁UM)∩(∁UN) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com