【題目】如圖，在三棱柱
中，平面
平面
，四邊形
是正方形，點
，
分別是棱
，
的中點，
，
，
.
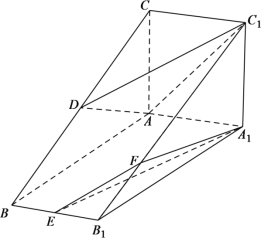
（1）求證：
；
（2）求二面角
的余弦值；
（3）若點
在棱
上，且
，判斷平面
與平面
是否平行，并說明理由.
【答案】（1）證明見解析（2）
（3）平面
與平面
不平行；詳見解析
【解析】
（1）根據平面
平面
和
得
平面.，得
；
（2）以
為原點，建立空間直角坐標系
，根據兩個半平面的法向量可求得結果；
（3）根據平面的法向量與向量
不垂直可得結論.
（1）證明：因為四邊形是正方形，所以.
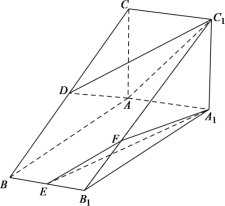
又因為平面平面，
平面
平面
，
所以平面.
又因為
平面，
所以.
（2）由（1）知，
，
，所以
.
又
，
，
，
所以
.所以
.
如圖，以為原點，建立空間直角坐標系.
所以
，
，
，
.
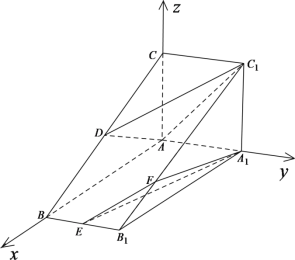
則有
，
，
，
平面
的一個法向量為
.
設平面的一個法向量為
，
又
，
，
由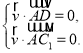
得
令
，則
，
.所以
.
設二面角
的平面角為
，則
.
由題知，二面角為銳角，所以其余弦值為.
（3）平面與平面不平行.理由如下：
由（2）知，平面的一個法向量為，
，
所以
，所以
與平面不平行.
又因為
平面，
所以平面與平面不平行.
科目：高中數學 來源： 題型：
【題目】已知函數
（1）求函數
的極值點；
（2）定義：若函數的圖像與直線
有公共點，我們稱函數有不動點.這里取：
，若
，如果函數
存在不動點，求實數
取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，給出下列四個結論：
①函數
的最小正周期是
；
②函數在區間
上是減函數；
③函數的圖象關于直線
對稱；
④函數的圖象可由函數
的圖象向左平移
個單位得到其中所有正確結論的編號是（ ）
A.①②B.①③C.①②③D.①③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
中，底面
為正方形，
平面
，
，點
為線段
的動點．記
與
所成角的最小值為
，當為線段中點時，二面角
的大小為
，二面角
的大小為
，則，，的大小關系是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知：在長方體
中，
，點
是線段
上的一個動點，則①
的最小值等于__________；②直線
與平面
所成角的正切值的取值范圍為____________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對全國互聯網行業進行調查統計，得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業者崗位分布條形圖，則下列結論中不一定正確的是( ).
注：90后指1990年及以后出生，80后指1980-1989年之間出生，80前指1979年及以前出生.
A. 互聯網行業從業人員中90后占一半以上
B. 互聯網行業中從事技術崗位的人數超過總人數的20%
C. 互聯網行業中從事運營崗位的人數90后比80前多
D. 互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一個有窮數列的每相鄰兩項之間插入這兩項的和，形成新的數列，我們把這樣的操作稱為該數列的一次“Z拓展”.如數列1，2第1次“Z拓展”后得到數列1，3，2，第2次“Z拓展”后得到數列1，4，3，5，2.設數列a，b，c經過第n次“Z拓展”后所得數列的項數記為Pn，所有項的和記為Sn.
（1）求P1，P2；
（2）若Pn≥2020，求n的最小值；
（3）是否存在實數a，b，c，使得數列{Sn}為等比數列？若存在，求a，b，c滿足的條件；若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com