
【題目】已知函數![]() .
.
(1)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)函數![]() 在區間
在區間![]() 上有零點,求
上有零點,求![]() 的值;
的值;
(3)若不等式![]() 對任意正實數
對任意正實數![]() 恒成立,求正整數
恒成立,求正整數![]() 的取值集合.
的取值集合.
【答案】(1) ![]() ;(2)
;(2) ![]() 的值為0或3 ;(3)
的值為0或3 ;(3) ![]() .
.
【解析】
(1)由![]() 的值可得切點坐標,求出
的值可得切點坐標,求出![]() 的值,可得切線斜率,利用點斜式可得曲線
的值,可得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(2)先利用導數判斷函數的單調性,然后根據零點存在定理可判斷
處的切線方程;(2)先利用導數判斷函數的單調性,然后根據零點存在定理可判斷![]() 在區間
在區間![]() 、
、![]() 上分別存在一個零點,從而可得結果;(3)當
上分別存在一個零點,從而可得結果;(3)當![]() 時,不等式為
時,不等式為![]() 恒成立;當
恒成立;當![]() 時,不等式可化為
時,不等式可化為![]() ,可得
,可得![]() ,當
,當![]() 時,不等式可化為
時,不等式可化為![]() ,可得
,可得![]() ,結合(2),綜合三種情況,從而可得結果.
,結合(2),綜合三種情況,從而可得結果.
(1)![]() ,所以切線斜率為
,所以切線斜率為![]() ,
,
又![]() ,切點為
,切點為![]() ,所以切線方程為
,所以切線方程為![]() .
.
(2)令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,
單調遞增,
所以![]() 的極小值為
的極小值為![]() ,又
,又![]() ,
,
所以![]() 在區間
在區間![]() 上存在一個零點
上存在一個零點![]() ,此時
,此時![]() ;
;
因為![]() ,
,![]() ,
,
所以![]() 在區間
在區間![]() 上存在一個零點
上存在一個零點![]() ,此時
,此時![]() .綜上,
.綜上,![]() 的值為0或3.
的值為0或3.
(3)當![]() 時,不等式為
時,不等式為![]() .顯然恒成立,此時
.顯然恒成立,此時![]() ;
;
當![]() 時,不等式
時,不等式![]() 可化為
可化為![]() ,
,
令![]() ,則
,則![]() ,
,
由(2)可知,函數![]() 在
在![]() 上單調遞減,且存在一個零點
上單調遞減,且存在一個零點![]() ,
,
此時![]() ,即
,即![]()
所以當![]() 時,
時,![]() ,即
,即![]() ,函數
,函數![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() ,即
,即![]() ,函數
,函數![]() 單調遞減.
單調遞減.
所以![]() 有極大值即最大值
有極大值即最大值![]() ,于是
,于是![]() .
.
當![]() 時,不等式
時,不等式![]() 可化為
可化為![]() ,
,
由(2)可知,函數![]() 在
在![]() 上單調遞增,且存在一個零點
上單調遞增,且存在一個零點![]() ,同理可得
,同理可得![]() .
.
綜上可知![]() .
.
又因為![]() ,所以正整數
,所以正整數![]() 的取值集合為
的取值集合為![]() .
.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:高中數學 來源: 題型:
【題目】學校科技小組在計算機上模擬航天器變軌返回試驗,設計方案如圖:航天器運行(按順時針方向)的軌跡方程為![]() ,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以
,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以![]() 軸為對稱軸、
軸為對稱軸、![]() 為頂點的拋物線的實線部分,降落點為
為頂點的拋物線的實線部分,降落點為![]() .觀測點
.觀測點![]() 、
、![]() 同時跟蹤航天器.
同時跟蹤航天器.
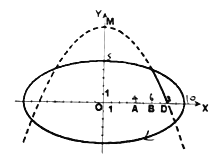
(1)求航天器變軌后的運行軌跡所在的曲線方程;
(2)試問:當航天器在![]() 軸上方時,觀測點
軸上方時,觀測點![]() 、
、![]() 測得離航天器的距離分別為多少時,應向航天器發出變軌指令?
測得離航天器的距離分別為多少時,應向航天器發出變軌指令?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年2月13日《煙臺市全民閱讀促進條例》全文發布,旨在保障全民閱讀權利,培養全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.

(1)求這200名學生每周閱讀時間的樣本平均數![]() 和中位數
和中位數![]() (
(![]() 的值精確到0.01);
的值精確到0.01);
(2)為查找影響學生閱讀時間的因素,學校團委決定從每周閱讀時間為![]() ,
,![]() 的學生中抽取9名參加座談會.
的學生中抽取9名參加座談會.
(i)你認為9個名額應該怎么分配?并說明理由;
(ii)座談中發現9名學生中理工類專業的較多.請根據200名學生的調研數據,填寫下面的列聯表,并判斷是否有![]() 的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?
的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?
閱讀時間不足8.5小時 | 閱讀時間超過8.5小時 | |
理工類專業 | 40 | 60 |
非理工類專業 |
附:![]() (
(![]() ).
).
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| <> | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在極坐標系(與平面直角坐標系
為參數).在極坐標系(與平面直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,直線
軸非負半軸為極軸)中,直線![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的普通方程及直線
的普通方程及直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,求
點,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com