
【題目】函數![]() 是R上的奇函數,m、n是常數.
是R上的奇函數,m、n是常數.
(1)求m,n的值;
(2)判斷![]() 的單調性并證明;
的單調性并證明;
(3)不等式![]() 對任意
對任意![]() 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
【答案】(1)![]() ;(2)在R上遞增,證明見解析;(3)
;(2)在R上遞增,證明見解析;(3)![]()
【解析】
(1)依題意![]() 時
時![]() 上的奇函數,則采用特殊值法,
上的奇函數,則采用特殊值法,![]() 即可求出參數的值;
即可求出參數的值;
(2)利用定義法證明函數的單調性,按照:設元、作差、變形、判斷符號、下結論的步驟完成即可;
(3)根據函數的奇偶性和單調性將函數不等式轉化為自變量的不等式,即![]() 對任意
對任意![]() 恒成立,令
恒成立,令![]() ,即
,即![]() ,對
,對![]() 恒成立,令
恒成立,令![]() ,根據二次函數的性質分析可得;
,根據二次函數的性質分析可得;
解:(1)∵![]() 是
是![]() 上的奇函數,
上的奇函數,
∴![]() ∴
∴![]()
∴![]() .
.
(2)![]() 在
在![]() 上遞增
上遞增
證明:設![]() ,且
,且![]() ,則
,則
 ,
,
∵![]() ∴
∴![]() 又
又![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() 是
是![]() 上的增函數.
上的增函數.
(3)由題意得:![]() 對任意
對任意![]() 恒成立又
恒成立又![]() 是R上的增函數,
是R上的增函數,
∴![]() 即
即![]() 對任意
對任意![]() 恒成立,
恒成立,
令![]() ,即
,即![]() ,對
,對![]() 恒成立,令
恒成立,令![]() ,對稱軸為
,對稱軸為![]() ,當
,當![]() 即
即![]() 時,
時,![]() 在
在![]() 為增函數,
為增函數,
∴![]() 成立,∴
成立,∴![]() 符合,
符合,
當![]() 即
即![]() 時,
時,![]() 在
在![]() 為減,
為減,![]() 為增,
為增,
∴![]()
解得![]() ,∴
,∴![]() .
.
綜上![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設x,y,z為空間不同的直線或不同的平面,且直線不在平面內,下列說法能保證“若![]() ,
,![]() ,則
,則![]() ”為真命題的序號為______.
”為真命題的序號為______.
①x為直線,y,z為平面;
②x,y,z都為平面;
③x,y為直線,z為平面;
④x,y,z都為直線;
⑤x,y為平面,z為直線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調遞增與單調遞減區間(直接寫結果);
的單調遞增與單調遞減區間(直接寫結果);
(2)當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,試求實數m的取值范圍;
,試求實數m的取值范圍;
(3)若不等式![]() 對任意
對任意![]() ,
,![]() 恒成立,求實數b的取值范圍.
恒成立,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟的發展,個人收入的提高,自2019年1月1日起,個人所得稅起征點和稅率的調整,調整如下:納稅人的工資、薪金所得,以每月全部收入額減除5000元后的余額為應納稅所得額,依照個人所得稅稅率表,調整前后的計算方法如下表:

(1)假如小紅某月的工資、薪金等所得稅前收入總和不高于8000元,記![]() 表示總收入,
表示總收入,![]() 表示應納的稅,試寫出調整前后
表示應納的稅,試寫出調整前后![]() 關于
關于![]() 的函數表達式;
的函數表達式;
(2)某稅務部門在小紅所在公司利用分層抽樣方法抽取某月100個不同層次員工的稅前收入,并制成下面的頻數分布表:

①先從收入在![]() 及
及![]() 的人群中按分層抽樣抽取7人,再從中選4人作為新納稅法知識宣講員,用
的人群中按分層抽樣抽取7人,再從中選4人作為新納稅法知識宣講員,用![]() 表示抽到作為宣講員的收入在
表示抽到作為宣講員的收入在![]() 元的人數,
元的人數,![]() 表示抽到作為宣講員的收入在
表示抽到作為宣講員的收入在![]() 元的人數,隨機變量
元的人數,隨機變量![]() ,求
,求![]() 的分布列與數學期望;
的分布列與數學期望;
②小紅該月的工資、薪金等稅前收入為7500元時,請你幫小紅算一下調整后小紅的實際收入比調整前增加了多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解本市的交通狀況,某校高一年級的同學分成了甲、乙、丙三個組,從下午13點到18點,分別對三個路口的機動車通行情況進行了實際調查,并繪制了頻率分布直方圖(如圖),記甲、乙、丙三個組所調查數據的標準差分別為![]() ,則它們的大小關系為( )
,則它們的大小關系為( )



A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(多選)統計某校![]() 名學生的某次數學同步練習成績(滿分150分),根據成績依次分成六組:
名學生的某次數學同步練習成績(滿分150分),根據成績依次分成六組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到頻率分布直方圖如圖所示,若不低于140分的人數為110,則下列說法正確的是( )
,得到頻率分布直方圖如圖所示,若不低于140分的人數為110,則下列說法正確的是( )
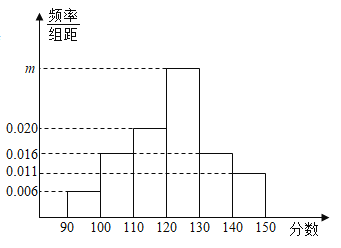
A.![]() B.
B.![]()
C.100分以下的人數為60D.成績在區間![]() 內的人數占大半
內的人數占大半
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級有50名學生,其中有30名男生和20名女生,隨機詢問了該班5名男生和5名女生在某次數學測驗中的成績,5名男生的成績分別為86,94,88,92,90,5名女生的成績分別為88,93,93,88,93.
①這種抽樣方法是一種分層隨機抽樣;
②這5名男生成績的方差大于這5名女生成績的方差;
③該班男生成績的平均數小于該班女生成績的平均數.
則以上說法一定正確的是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖:
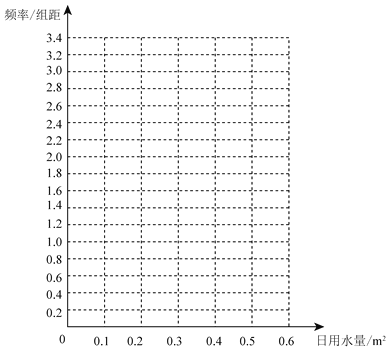
(2)估計該家庭使用節水龍頭后,日用水量小于0.35 m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點坐標分別是
的兩個焦點坐標分別是![]() 、
、![]() ,并且經過點
,并且經過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() :
:![]() 相切,并與橢圓
相切,并與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() .當
.當![]() ,且滿足
,且滿足![]() 時,求
時,求![]() 面積
面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com