
【題目】已知橢圓C: ![]() =1(a>b>0)的左右焦點分別為F1 , F2 , 點
=1(a>b>0)的左右焦點分別為F1 , F2 , 點 ![]() 為短軸的一個端點,∠OF2B=60°.
為短軸的一個端點,∠OF2B=60°.
(Ⅰ)求橢圓C的方程;
(Ⅱ)如圖,過右焦點F2 , 且斜率為k(k≠0)的直線l與橢圓C相交于D,E兩點,A為橢圓的右頂點,直線AE,AD分別交直線x=3于點M,N,線段MN的中點為P,記直線PF2的斜率為k′.試問kk′是否為定值?若為定值,求出該定值;若不為定值,請說明理由.
【答案】解:(1)由條件可知 ![]() ,故所求橢圓方程為
,故所求橢圓方程為 ![]() .(2)設過點F2(1,0)的直線l方程為:y=k(x﹣1).
.(2)設過點F2(1,0)的直線l方程為:y=k(x﹣1).
由 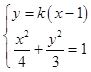 可得:(4k2+3)x2﹣8k2x+4k2﹣12=0
可得:(4k2+3)x2﹣8k2x+4k2﹣12=0
因為點F2(1,0)在橢圓內,所以直線l和橢圓都相交,即△>0恒成立.
設點E(x1 , y1),D(x2 , y2),
則 ![]() .
.
因為直線AE的方程為: ![]() ,直線AD的方程為:
,直線AD的方程為: ![]() ,
,
令x=3,可得 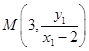 ,
, 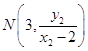 ,所以點P的坐標
,所以點P的坐標 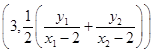 .
.
直線PF2的斜率為 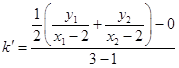 =
= 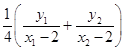 =
= ![]() =
= ![]() =
= 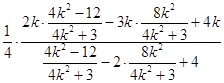
= ![]() ,
,
所以kk'為定值 ![]() .
.
【解析】(1)由條件可知 ![]() ,故求的橢圓方程.(2)設過點F2(1,0)的直線l方程為:y=k(x﹣1).由
,故求的橢圓方程.(2)設過點F2(1,0)的直線l方程為:y=k(x﹣1).由 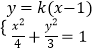 可得:(4k2+3)x2﹣8k2x+4k2﹣12=0.因為直線AE的方程為:
可得:(4k2+3)x2﹣8k2x+4k2﹣12=0.因為直線AE的方程為: ![]() ,直線AD的方程為:
,直線AD的方程為: ![]() ,從而列式求解即可.
,從而列式求解即可.


科目:高中數學 來源: 題型:
【題目】在甲、乙兩個盒子中分別裝有標號為1、2、3、4的四個球,現從甲、乙兩個盒子中各取出1個球,每個小球被取出的可能性相等.
(Ⅰ)求取出的兩個球上標號為相鄰整數的概率;
(Ⅱ)求取出的兩個球上標號之和能被3整除的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】口袋中裝有一些大小相同的紅球和黑球,從中取出2個球.兩個球都是紅球的概率是 ![]() ,都是黑球的概率是
,都是黑球的概率是 ![]() ,則取出的2個球中恰好一個紅球一個黑球的概率是( )
,則取出的2個球中恰好一個紅球一個黑球的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在△ABC中,角A、B、C所對應的邊為a,b,c. (I)若sin(A+ ![]() )=
)= ![]() cosA,求A的值;
cosA,求A的值;
(Ⅱ)若cosA= ![]() ,b=3c,求sinC的值.
,b=3c,求sinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設S表示所有大于﹣1的實數構成的集合,確定所有的函數:S→S,滿足以下兩個條件:
對于S內的所有x和y,f(x+f(y)+xf(y))=y+f(x)+yf(x);在區間﹣1<x<0與x>0的每一個內, ![]() 是嚴格遞增的.求滿足上述條件的函數的方程.
是嚴格遞增的.求滿足上述條件的函數的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等比數列,a1=2,a3=18.數列{bn}是等差數列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求數列{an},{bn}的通項公式;
(2)設Pn=b1+b4+b7+…+b3n﹣2 , Qn=b10+b12+b14+…+b2n+8 , 其中n=1,2,3,….試比較Pn與Qn的大小,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com