選修4-4:坐標系與參數方程
從極點O作射線,交直線ρcosθ=3于點M,P為射線OM上的點,且|OM|•|OP|=12,若有且只有一個點P在直線ρsinθ-ρcosθ=m,求實數m的值.
【答案】
分析:設P(ρ,θ),由條件|OM|•|OP|=12,可求出點M的坐標,由于點M在直線ρ
′cosθ=3上,可將點M的坐標代入得出點P的極坐標方程,進而化為直角坐標系的方程,知道點P的軌跡是一個圓且去掉x軸上的兩點.因為有且只有一個點P在直線
ρsinθ-ρcosθ=m上,故直線與圓相切,或直線經過原點,據此可求實數m的值.
解答:解:設P(ρ,θ),則由|OM||OP|=12得|OM|=
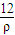
,∴
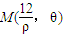
,由于點M在直線ρ
′cosθ=3上,∴
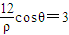
.
即ρ=4cosθ(ρ≠0).
∴ρ
2=4ρcosθ,化為平面直角坐標系的方程為x
2+y
2=4x,即(x-2)
2+y
2=4(x≠0).
直線ρsinθ-ρcosθ=m化為平面直角坐標系的方程為y-x-m=0,
因為有且只有一個點P在直線y-x-m=0上,所以y-x-m=0和(x-2)
2+y
2=4(x≠0)相切,
∴
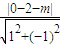
=2,解得m=-2±
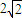
.
或直線l過原點時也滿足條件,此時m=0.
總上可知:m的取值是-2±
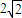
,或0.
點評:本題考查了極坐標系下直線與圓的交點問題,將極坐標化為直角坐標系的方程是解決此問題常用的方法.

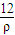 ,∴
,∴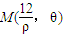 ,由于點M在直線ρ′cosθ=3上,∴
,由于點M在直線ρ′cosθ=3上,∴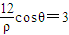 .
.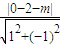 =2,解得m=-2±
=2,解得m=-2±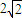 .
.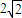 ,或0.
,或0.

 名校課堂系列答案
名校課堂系列答案 A.選修4-1:幾何證明選講
A.選修4-1:幾何證明選講