
(本題滿分8分)探究函數![]() 的最小值,并確定相應的x的值,列表如下:
的最小值,并確定相應的x的值,列表如下:
| x | … |
|
| 1 |
| 2 |
| 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 |
| 4 |
| 5 | 8.5 | 16.25 | … |
請觀察表中y值隨x值變化的特點,完成下列問題:
(Ⅰ)若![]() ,則
,則![]()
![]() (請填寫“>, =, <”號);若函數
(請填寫“>, =, <”號);若函數![]() ,(x>0)在區間(0,2)上遞減,則在 上遞增;
,(x>0)在區間(0,2)上遞減,則在 上遞增;
(Ⅱ)當x= 時,![]() ,(x>0)的最小值為 ;
,(x>0)的最小值為 ;
(Ⅲ)試用定義證明![]() ,(x>0)在區間(0,2)上遞減.
,(x>0)在區間(0,2)上遞減.
 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源:2014屆廣東省高一上學期期中試題數學 題型:解答題
(本題滿分12分)探究函數 的最小值,并確定取得最小值時x的值. 列表如下, 請觀察表中y值隨x值變化的特點,完成以下的問題.
的最小值,并確定取得最小值時x的值. 列表如下, 請觀察表中y值隨x值變化的特點,完成以下的問題.
|
x |
… |
0.25 |
0.5 |
0.75 |
1 |
1.1 |
1.2 |
1.5 |
2 |
3 |
5 |
… |
|
y |
… |
8.063 |
4.25 |
3.229 |
3 |
3.028 |
3.081 |
3.583 |
5 |
9.667 |
25.4 |
… |
已知:函數 在區間(0,1)上遞減,問:
在區間(0,1)上遞減,問:
(1)函數 在區間
上遞增.當
在區間
上遞增.當 時,
時, ;
;
(2)函數 在定義域內有最大值或最小值嗎?如有,是多少?此時x為何值?(直接回答結果,不需證明)
在定義域內有最大值或最小值嗎?如有,是多少?此時x為何值?(直接回答結果,不需證明)
查看答案和解析>>
科目:高中數學 來源:2010年海南省高一期中考試數學試卷 題型:解答題
((本題滿分8分)探究函數 的最小值,并確定相應的x的值,列表如下:
的最小值,并確定相應的x的值,列表如下:
|
x |
… |
|
|
1 |
|
2 |
|
4 |
8 |
16 |
… |
|
y |
… |
16.25 |
8.5 |
5 |
|
4 |
|
5 |
8.5 |
16.25 |
… |
請觀察表中y值隨x值變化的特點,完成下列問題:
(Ⅰ)若 ,則
,則
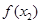 (請填寫“>, =, <”號);若函數
(請填寫“>, =, <”號);若函數 ,(x>0)在區間(0,2)上遞減,則在 上遞增;
,(x>0)在區間(0,2)上遞減,則在 上遞增;
(Ⅱ)當x= 時, ,(x>0)的最小值為
;
,(x>0)的最小值為
;
(Ⅲ)試用定義證明 ,(x>0)在區間(0,2)上遞減.
,(x>0)在區間(0,2)上遞減.
查看答案和解析>>
科目:高中數學 來源:2010年河北省高一上學期期中考試數學試卷 題型:解答題
(本題滿分12分)探究函數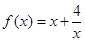 ,
,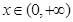 的最小值,并確定取得最小值時
的最小值,并確定取得最小值時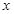 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
請觀察表中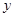 值隨
值隨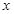 值變化的特點,完成下列問題:
值變化的特點,完成下列問題:
(1) 當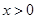 時,
時,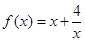 在區間
在區間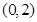 上遞減,在區間 上遞增;
上遞減,在區間 上遞增;
所以,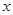 =
時,
=
時, 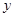 取到最小值為
;
取到最小值為
;
(2) 由此可推斷,當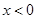 時,
時,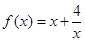 有最
值為 ,此時
有最
值為 ,此時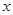 =
;
=
;
(3) 證明: 函數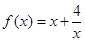 在區間
在區間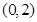 上遞減;
上遞減;
(4) 若方程 在
在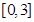 內有兩個不相等的實數根,求實數
內有兩個不相等的實數根,求實數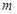 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分12分)探究函數![]() ,
,![]() 的最小值,并確定取得最小值時
的最小值,并確定取得最小值時![]() 的值,列表如下:
的值,列表如下:
|
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
|
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
請觀察表中![]() 值隨
值隨![]() 值變化的特點,完成下列問題:
值變化的特點,完成下列問題:
(1) 當![]() 時,
時,![]() 在區間
在區間![]() 上遞減,在區間 上遞增;
上遞減,在區間 上遞增;
所以,![]() = 時,
= 時, ![]() 取到最小值為 ;
取到最小值為 ;
(2) 由此可推斷,當![]() 時,
時,![]() 有最 值為 ,此時
有最 值為 ,此時![]() = ;
= ;
(3) 證明: 函數![]() 在區間
在區間![]() 上遞減;
上遞減;
(4) 若方程![]() 在
在![]() 內有兩個不相等的實數根,求實數
內有兩個不相等的實數根,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com