
規(guī)定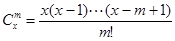 ,其中x∈R,m是正整數(shù),且
,其中x∈R,m是正整數(shù),且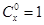 ,這是組合數(shù)
,這是組合數(shù)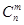 (n、m是正整數(shù),且m≤n)的一種推廣.
(n、m是正整數(shù),且m≤n)的一種推廣.
(1) 求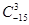 的值;
的值;
(2) 設(shè)x>0,當(dāng)x為何值時,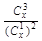 取得最小值?
取得最小值?
(3) 組合數(shù)的兩個性質(zhì);
①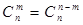 . ②
. ②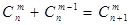 .
.
是否都能推廣到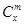 (x∈R,m是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
(x∈R,m是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
(1)-680(2)
(3)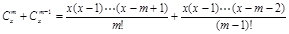
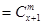
【解析】
試題分析:解:(1) .
.
(2)  . ∵ x > 0 ,
. ∵ x > 0 ,  .
.
當(dāng)且僅當(dāng) 時,等號成立. ∴ 當(dāng)
時,等號成立. ∴ 當(dāng) 時,
時,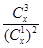 取得最小值.
取得最小值.
(3)性質(zhì)①不能推廣,例如當(dāng) 時,
時,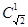 有定義,但
有定義,但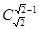 無意義;
無意義;
性質(zhì)②能推廣,它的推廣形式是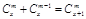 ,xÎR , m是正整數(shù).
,xÎR , m是正整數(shù).
事實(shí)上,當(dāng)m=1時,有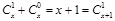 .
.
當(dāng)m≥2時. 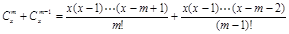

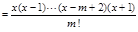
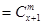 .
.
考點(diǎn):組合數(shù)公式和性質(zhì)
點(diǎn)評:主要是考查了組合數(shù)的公式的靈活的變換和求解運(yùn)算能力,屬于基礎(chǔ)題。



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
規(guī)定![]() ,其中x∈R,m是正整數(shù),且
,其中x∈R,m是正整數(shù),且![]() =1,這是組合數(shù)
=1,這是組合數(shù)![]() (n、m是正整數(shù),且m≤n)的一種推廣。
(n、m是正整數(shù),且m≤n)的一種推廣。
(I)求![]() 的值。
的值。
(II)組合數(shù)的兩個性質(zhì);①![]() ;②
;②![]() 。是否都能推廣到
。是否都能推廣到![]() (x∈R,m是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由;
(x∈R,m是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
規(guī)定![]() =
=![]() ,其中x∈R,m是正整數(shù),且
,其中x∈R,m是正整數(shù),且![]() ,這是組合數(shù)
,這是組合數(shù)![]() (n、m是正整數(shù),且m≤n)的一種推廣.
(n、m是正整數(shù),且m≤n)的一種推廣.
(1)求![]() 的值.
的值.
(2)設(shè)x>0,當(dāng)x為何值時,![]() 取最小值?
取最小值?
(3)我們知道組合數(shù)具有如下兩個性質(zhì):
①![]() =
=![]() ;②
;②![]() +
+![]() =
=![]() .
.
是否都能推廣到![]() (x∈R,m是正整數(shù))的情形?若能推廣,請寫出推廣的形式,并給出證明;若不能,則說明理由.
(x∈R,m是正整數(shù))的情形?若能推廣,請寫出推廣的形式,并給出證明;若不能,則說明理由.
(4)已知組合數(shù)![]() 是正整數(shù),證明當(dāng)x∈Z,m是正整數(shù)時,
是正整數(shù),證明當(dāng)x∈Z,m是正整數(shù)時,![]() ∈Z.
∈Z.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012年人教A版高中數(shù)學(xué)選修2-3 1.3二項(xiàng)式定理練習(xí)卷(解析版) 題型:解答題
(14分)規(guī)定 ,其中x∈R,m是正整數(shù),且
,其中x∈R,m是正整數(shù),且 ,這是組合數(shù)
,這是組合數(shù) (n、m是正整數(shù),且m≤n)的一種推廣.
(n、m是正整數(shù),且m≤n)的一種推廣.
(1) 求 的值;
的值;
(2) 設(shè)x>0,當(dāng)x為何值時, 取得最小值?
取得最小值?
(3) 組合數(shù)的兩個性質(zhì);
① . ②
. ② .
.
是否都能推廣到 (x∈R,m是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
(x∈R,m是正整數(shù))的情形?若能推廣,則寫出推廣的形式并給出證明;若不能,則說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:專項(xiàng)題 題型:解答題
 ,其中x∈R,m是正整數(shù),且
,其中x∈R,m是正整數(shù),且 ,這是組合數(shù)
,這是組合數(shù) (n,m是正整數(shù),且m≤n)的一種推廣,
(n,m是正整數(shù),且m≤n)的一種推廣, 的值;
的值; ;②
;② ,
, (x∈R,m是正整數(shù))的情形?若能推廣,請寫出推廣的形式,并給出明;若不能,則說明理由;
(x∈R,m是正整數(shù))的情形?若能推廣,請寫出推廣的形式,并給出明;若不能,則說明理由;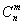 是正整數(shù),證明:當(dāng)x∈Z,m是正整數(shù)時,
是正整數(shù),證明:當(dāng)x∈Z,m是正整數(shù)時, ∈Z。
∈Z。 查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com