
【題目】設橢圓![]() :
:![]() (
(![]() ),左、右焦點分別是
),左、右焦點分別是![]() 、
、![]() 且
且![]() ,以
,以![]() 為圓心,3為半徑的圓與以
為圓心,3為半徑的圓與以![]() 為圓心,1為半徑的圓相交于橢圓
為圓心,1為半徑的圓相交于橢圓![]() 上的點
上的點![]()
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() :
:![]() ,
,![]() 為橢圓
為橢圓![]() 上任意一點,過點
上任意一點,過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,射線
兩點,射線![]() 交橢圓
交橢圓![]() 于點
于點![]()
①求![]() 的值;
的值;
②令![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)運用圓與圓的位置關系,![]() 和
和![]() 的關系,計算即可得到
的關系,計算即可得到![]() ,進而得到橢圓
,進而得到橢圓![]() 的方程;
的方程;
(2)求得橢圓![]() 的方程,①設
的方程,①設![]() ,
,![]() ,求得
,求得![]() 的坐標,分別代入橢圓
的坐標,分別代入橢圓![]() 的方程,化簡整理,即可得到所求值;
的方程,化簡整理,即可得到所求值;
②設![]() ,
,![]() 將直線
將直線![]() 代入橢圓
代入橢圓![]() 的方程,運用韋達定理,三角形的面積公式,將直線
的方程,運用韋達定理,三角形的面積公式,將直線![]() 代入橢圓
代入橢圓![]() 的方程,由判別式大于0,可得
的方程,由判別式大于0,可得![]() 的范圍,結合二次函數的最值,,
的范圍,結合二次函數的最值,,![]() 的面積為
的面積為![]() ,即可得到所求的最大值.
,即可得到所求的最大值.
解:(1)由題意可知,![]() ,可得
,可得![]() ,
,
又![]()
![]() ,
,
![]() ,
,
![]()
即有橢圓![]() 的方程為
的方程為![]() ;
;
(2)由(1)知橢圓![]() 的方程為
的方程為![]() ,
,
①設![]() ,
,![]() ,由題意可知,
,由題意可知,
![]() ,由于
,由于![]() ,
,
代入化簡可得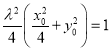 ,
,
所以![]() ,即
,即![]() ;
;
②設![]() ,
,![]() ,將直線
,將直線![]() 代入橢圓
代入橢圓![]() 的方程,可得
的方程,可得
![]()
![]() ,由
,由![]() ,可得
,可得![]() ,③
,③
則有![]() ,
,![]() ,
,
所以![]() ,
,
由直線![]() 與
與![]() 軸交于
軸交于![]() ,
,
則![]() 的面積為
的面積為![]()
![]()
設![]() ,則
,則![]() ,
,
將直線![]() 代入橢圓
代入橢圓![]() 的方程,
的方程,
可得![]()
![]() ,
,
由![]() 可得
可得![]() ,④
,④
由③④可得![]() ,則
,則![]() 在
在![]() 遞增,即有
遞增,即有![]() 取得最大值,
取得最大值,
即有![]() ,即
,即![]() ,取得最大值
,取得最大值![]() ,
,
由①知,![]() 的面積為
的面積為![]() ,
,
即![]() 面積的最大值為
面積的最大值為![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的離心率
)的離心率![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,過右焦點
,過右焦點![]() 任作一條不垂直于坐標軸的直線l與橢圓C交于A,B兩點,
任作一條不垂直于坐標軸的直線l與橢圓C交于A,B兩點,![]() 的周長為
的周長為![]() .
.
(1)求橢圓C的方程;
(2)記點B關于x軸的對稱點為![]() 點,直線
點,直線![]() 交x軸于點D.求
交x軸于點D.求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到其焦點下的距離為10.
到其焦點下的距離為10.
(1)求拋物線C的方程;
(2)設過焦點F的的直線![]() 與拋物線C交于
與拋物線C交于![]() 兩點,且拋物線在
兩點,且拋物線在![]() 兩點處的切線分別交x軸于
兩點處的切線分別交x軸于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直線PB與CD所成角的大小為![]() ,求BC的長;
,求BC的長;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電子計算機誕生于20世紀中葉,是人類最偉大的技術發明之一.計算機利用二進制存儲信息,其中最基本單位是“位(bit)”,1位只能存放2種不同的信息:0或l,分別通過電路的斷或通實現.“字節(Byte)”是更大的存儲單位,1Byte=8bit,因此1字節可存放從00000000(2)至11111111(2)共256種不同的信息.將這256個二進制數中,所有恰有相鄰兩位數是1其余各位數均是0的所有數相加,則計算結果用十進制表示為
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一塊黃銅板上插著三根寶石針,在其中一根針上從下到上穿好由大到小的若干金片.若按照下面的法則移動這些金片:每次只能移動一片金片;每次移動的金片必須套在某根針上;大片不能疊在小片上面.設移完n片金片總共需要的次數為an,可推得a1=1,an+1=2an+1.如圖是求移動次數在1000次以上的最小片數的程序框圖模型,則輸出的結果是( )
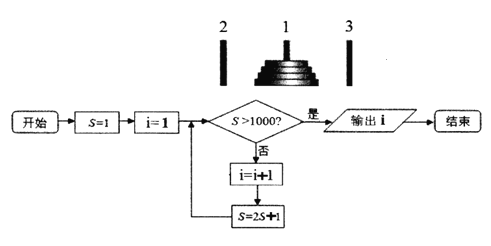
A. 8B. 9C. 10D. 11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 分別與直線
分別與直線![]() ,
,![]() 交于
交于![]() ,其中點
,其中點![]() 在第三象限,點
在第三象限,點![]() 在第二象限,點
在第二象限,點![]() ;
;
(1)若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)直線![]() 交于
交于![]() 點
點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() ,若
,若![]() 直線的斜率均存在,分別設為
直線的斜率均存在,分別設為![]() ,判斷
,判斷![]() 是否為定值?若為定值,求出該定值;若不為定值,說明理由.
是否為定值?若為定值,求出該定值;若不為定值,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com