
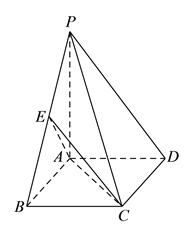
【題目】如圖所示,四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
(![]() )求證:
)求證: ![]() 平面
平面![]() .
.
(![]() )求證:平面
)求證:平面![]() 平面
平面![]() .
.
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐C﹣OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2 ![]() ,D為AB的中點.
,D為AB的中點. 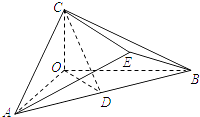
(Ⅰ)求證:AB⊥平面COD;
(Ⅱ)若動點E滿足CE∥平面AOB,問:當AE=BE時,平面ACE與平面AOB所成的銳二面角是否為定值?若是,求出該銳二面角的余弦值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2ax+5(a>1).
(1)若f(x)的定義域和值域均是[1,a],求實數a的值;
(2)若f(x)在區間(﹣∞,2]上是減函數,且對任意的x∈[1,a+1],總有f(x)≤0,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
(1)若對任意![]() ,且
,且![]() ,都有
,都有![]() ,則
,則![]() 為R上的減函數;
為R上的減函數;
(2)若![]() 為R上的偶函數,且在
為R上的偶函數,且在![]() 內是減函數,
內是減函數, ![]() (-2)=0,則
(-2)=0,則![]() >0解集為(-2,2);
>0解集為(-2,2);
(3)若![]() 為R上的奇函數,則
為R上的奇函數,則![]() 也是R上的奇函數;
也是R上的奇函數;
(4)t為常數,若對任意的![]() ,都有
,都有![]() 則
則![]() 關于
關于![]() 對稱。
對稱。
其中所有正確的結論序號為_________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】濮陽市黃河灘區某村2010年至2016年人均純收入(單位:萬元)的數據如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代號x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y關于x的線性回歸方程;
(Ⅱ)利用(Ⅰ)中的回歸方程,分析2010年至2016年該村人均純收入的變化情況,并預測該村2017年人均純收入.
附:回歸直線的斜率和截距的最小乘法估計公式分別為: ![]() =
= 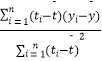 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,多面體PABCD的直觀圖及三視圖如圖所示,E、F分別為PC、BD的中點.

(I)求證:EF∥平面PAD;
(II)求證:平面PDC⊥平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦點分別為F1、F2 , |F1F2|=4,P是雙曲線右支上一點,直線PF2交y軸于點A,△APF1的內切圓切邊PF1于點Q,若|PQ|=1,則雙曲線的離心率為 .
=1(a>0,b>0)的左、右焦點分別為F1、F2 , |F1F2|=4,P是雙曲線右支上一點,直線PF2交y軸于點A,△APF1的內切圓切邊PF1于點Q,若|PQ|=1,則雙曲線的離心率為 . 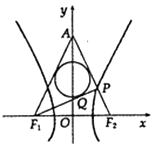
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f(x)圖象上不同兩點A(x1 , y1),B(x2 , y2)處的切線的斜率分別是kA , kB , 規定φ(A,B)= ![]() (|AB|為線段AB的長度)叫做曲線y=f(x)在點A與點B之間的“彎曲度”,給出以下命題: ①函數y=x3圖象上兩點A與B的橫坐標分別為1和﹣1,則φ(A,B)=0;
(|AB|為線段AB的長度)叫做曲線y=f(x)在點A與點B之間的“彎曲度”,給出以下命題: ①函數y=x3圖象上兩點A與B的橫坐標分別為1和﹣1,則φ(A,B)=0;
②存在這樣的函數,圖象上任意兩點之間的“彎曲度”為常數;
③設點A,B是拋物線y=x2+1上不同的兩點,則φ(A,B)≤2;
④設曲線y=ex(e是自然對數的底數)上不同兩點A(x1 , y1),B(x2 , y2),則φ(A,B)<1.
其中真命題的序號為 . (將所有真命題的序號都填上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com