
【題目】已知直線![]() 過點(diǎn)
過點(diǎn)![]() ,圓
,圓![]() :
:![]() .
.
(1)求截得圓![]() 弦長(zhǎng)最長(zhǎng)時(shí)
弦長(zhǎng)最長(zhǎng)時(shí)![]() 的直線方程;
的直線方程;
(2)若直線![]() 被圓N所截得的弦長(zhǎng)為
被圓N所截得的弦長(zhǎng)為![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】試題分析:(1)把圓N的方程化為標(biāo)準(zhǔn)方程,找出圓心![]() 的坐標(biāo),根據(jù)題意可知直線
的坐標(biāo),根據(jù)題意可知直線![]() 過圓心時(shí)截得的弦最長(zhǎng),故由
過圓心時(shí)截得的弦最長(zhǎng),故由![]() 及
及![]() 的坐標(biāo)確定出直線
的坐標(biāo)確定出直線![]() 的方程即可;(2)設(shè)直線
的方程即可;(2)設(shè)直線![]() 與圓
與圓![]() 交于
交于![]() 和
和![]() 兩點(diǎn)的坐標(biāo),過圓心
兩點(diǎn)的坐標(biāo),過圓心![]() 作
作![]() 垂直于
垂直于![]() ,根據(jù)垂徑定理得到
,根據(jù)垂徑定理得到![]() 為
為![]() 的中點(diǎn),從而得到
的中點(diǎn),從而得到![]() ,接下來(lái)分兩種情況考慮:第一,直線
,接下來(lái)分兩種情況考慮:第一,直線![]() 的斜率不存在時(shí),可得直線
的斜率不存在時(shí),可得直線![]() 的方程為
的方程為![]() ,把
,把![]() 代入圓
代入圓![]() 的方程中,得到關(guān)于
的方程中,得到關(guān)于![]() 的一元二次方程,求出方程的解得到
的一元二次方程,求出方程的解得到![]() 的值,經(jīng)過檢驗(yàn)得到
的值,經(jīng)過檢驗(yàn)得到![]() 時(shí),弦
時(shí),弦![]() 的長(zhǎng)為
的長(zhǎng)為![]() ,符合題意;第二,當(dāng)直線
,符合題意;第二,當(dāng)直線![]() 的斜率存在時(shí),設(shè)出直線
的斜率存在時(shí),設(shè)出直線![]() 的斜率為
的斜率為![]() ,由
,由![]() 的坐標(biāo)和設(shè)出的斜率
的坐標(biāo)和設(shè)出的斜率![]() 寫出直線
寫出直線![]() 的方程,在直角三角形
的方程,在直角三角形![]() 中,由
中,由![]() 的長(zhǎng)及半徑
的長(zhǎng)及半徑![]() 的長(zhǎng),利用勾股定理求出
的長(zhǎng),利用勾股定理求出![]() 的長(zhǎng),然后利用點(diǎn)到直線的距離公式表示出圓心
的長(zhǎng),然后利用點(diǎn)到直線的距離公式表示出圓心![]() 到直線
到直線![]() 的距離
的距離![]() ,令
,令![]() 等于求出的
等于求出的![]() 的長(zhǎng)列出關(guān)于
的長(zhǎng)列出關(guān)于![]() 的方程,求出方程的解得到
的方程,求出方程的解得到![]() 的值,確定出直線
的值,確定出直線![]() 的方程,綜上,得到所有滿足題意的直線
的方程,綜上,得到所有滿足題意的直線![]() 的方程.
的方程.
試題解析:(1)顯然,當(dāng)直線![]() 通過圓心N時(shí),被截得的弦長(zhǎng)最長(zhǎng),由
通過圓心N時(shí),被截得的弦長(zhǎng)最長(zhǎng),由![]() ,得
,得 ![]() 故所求直線
故所求直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
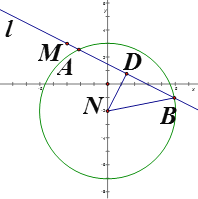
(2)設(shè)直線![]() 與圓N交于
與圓N交于![]() 兩點(diǎn)(如圖),作
兩點(diǎn)(如圖),作![]() 交直線
交直線![]() 于點(diǎn)D,顯然D為AB的中點(diǎn),且有
于點(diǎn)D,顯然D為AB的中點(diǎn),且有![]()
(Ⅰ)若直線![]() 的斜率不存在,則直線
的斜率不存在,則直線![]() 的方程為
的方程為![]() ,將
,將![]() 代入
代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
因此![]() 符合題意
符合題意
(Ⅱ)若直線![]() 的斜率存在,不妨設(shè)直線
的斜率存在,不妨設(shè)直線![]() 的方程為
的方程為 ![]() 即:
即: ![]() ,由
,由![]() ,得
,得![]() ,
, ![]() ,因此
,因此![]() ,又因?yàn)辄c(diǎn)N到直線
,又因?yàn)辄c(diǎn)N到直線![]() 的距離
的距離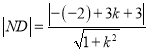
所以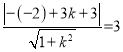 ,即:
,即: ![]() ,此時(shí)直線
,此時(shí)直線![]() 的方程為
的方程為![]() ,綜上可知,直線
,綜上可知,直線![]() 的方程為
的方程為![]() 或
或![]() .
.


 口算能手系列答案
口算能手系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了保護(hù)學(xué)生的視力,教室內(nèi)的日光燈在使用一段時(shí)間后必須更換.已知某校使用的100只日光燈在必須換掉前的使用天數(shù)如下表:
天數(shù)/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
燈管數(shù)/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)試估計(jì)這種日光燈的平均使用壽命;
(2)若定期更換,可選擇多長(zhǎng)時(shí)間統(tǒng)一更換合適?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]() 在區(qū)間[﹣
在區(qū)間[﹣ ![]() ,
, ![]() ]上有f(x)>0恒成立,則a的取值范圍為( )
]上有f(x)>0恒成立,則a的取值范圍為( )
A.(0,2]
B.[2,+∞)
C.(0,5)
D.(2,5]
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=x3﹣3x2 . (Ⅰ) 求f(x)的單調(diào)區(qū)間;
(Ⅱ) 若f(x)的定義域?yàn)閇﹣1,m]時(shí),值域?yàn)閇﹣4,0],求m的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() =
= ![]() ,其中
,其中![]() .
.
(1)證明:當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 在
在![]() 上為增函數(shù);
上為增函數(shù);
(2)設(shè)函數(shù)![]() =
= ![]() ,若函數(shù)
,若函數(shù)![]() 只有一個(gè)零點(diǎn),求實(shí)數(shù)
只有一個(gè)零點(diǎn),求實(shí)數(shù)![]() 的取值范圍,并求出該零點(diǎn)(可用
的取值范圍,并求出該零點(diǎn)(可用![]() 表示).
表示).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐P-ABC中,PA⊥AB,PA⊥BC,AB=BC,D為線段AC的中點(diǎn).

(1)求證:PA⊥BD.
(2)求證:BD⊥平面PAC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() ,且
,且![]() ,向量
,向量![]() ,
, ![]() .
.
(1)求函數(shù)![]() 的解析式,并求當(dāng)
的解析式,并求當(dāng)![]() 時(shí),
時(shí), ![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)當(dāng)![]() 時(shí),
時(shí), ![]() 的最大值為5,求
的最大值為5,求![]() 的值;
的值;
(3)當(dāng)![]() 時(shí),若不等式
時(shí),若不等式![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】一同學(xué)在電腦中打出如下若干個(gè)圈:○●○○●○○○●○○○○●○○○○○●…若將此若干個(gè)圈依此規(guī)律繼續(xù)下去,得到一系列的圈,那么在前55個(gè)圈中的●的個(gè)數(shù)是( )
A.10
B.9
C.8
D.11
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知隨機(jī)變量X~N(μ,σ2),且其正態(tài)曲線在(-∞,80)上是增函數(shù),在(80,+∞)上為減函數(shù),且P(72≤X≤88)=0.682 6.
(1)求參數(shù)μ,σ的值;
(2)求P(64<X≤72).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com