【題目】天壇公園是明、清兩代皇帝“祭天”“祈谷”的場所．天壇公園中的圜丘臺共有三層（如圖1所示），上層壇的中心是一塊呈圓形的大理石板，從中心向外圍以扇面形石（如圖2所示）．上層壇從第一環至第九環共有九環，中層壇從第十環至第十八環共有九環，下層壇從第十九環至第二十七環共有九環；第一環的扇面形石有9塊，從第二環起，每環的扇面形石塊數比前一環多9塊，則第二十七環的扇面形石塊數是______；上、中、下三層壇所有的扇面形石塊數是_______．
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為
，過點，斜率為1的直線與拋物線
交于點
，
，且
.
（1）求拋物線的方程；
（2）過點
作直線交拋物線于不同于
的兩點
、
，若直線
，
分別交直線
于
兩點，求
取最小值時直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙、丙三家企業產品的成本分別為10000，12000，15000，其成本構成如下圖所示，則關于這三家企業下列說法錯誤的是（ ）
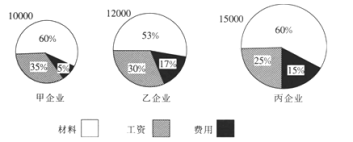
A.成本最大的企業是丙企業B.費用支出最高的企業是丙企業
C.支付工資最少的企業是乙企業D.材料成本最高的企業是丙企業
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個三角形數表按如下方式構成（如圖：其中項數
）：第一行是以4為首項，4為公差的等差數列，從第二行起，每一個數是其肩上兩個數的和，例如：
；
為數表中第
行的第
個數.
…
…
…
……
（1）求第2行和第3行的通項公式
和
；
（2）證明：數表中除最后2行外每一行的數都依次成等差數列，并求
關于
的表達式；
（3）若
，
，試求一個等比數列
，使得
，且對于任意的
，均存在實數
，當
時，都有
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體
中，平面
平面
．四邊形
為正方形，四邊形為梯形，且
，
，
，
．
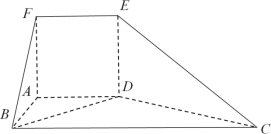
(1)求證：
；
(2)求直線
與平面
所成角的正弦值；
(3)線段
上是否存在點
，使得直線
平面
若存在，求
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校需要從甲、乙兩名學生中選一人參加數學競賽，抽取了近期兩人
次數學考試的成績，統計結果如下表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成績(分) |
|
|
|
|
|
乙的成績(分) |
|
|
|
|
|
(1)若從甲、乙兩人中選出一人參加數學競賽，你認為選誰合適?請說明理由.
(2)若數學競賽分初賽和復賽，在初賽中有兩種答題方案：
方案一：每人從道備選題中任意抽出
道，若答對，則可參加復賽，否則被淘汰.
方案二：每人從道備選題中任意抽出
道，若至少答對其中
道，則可參加復賽，否則被潤汰.
已知學生甲、乙都只會道備選題中的道，那么你推薦的選手選擇哪種答題方條進人復賽的可能性更大?并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
為橢圓
上任意一點，直線
與圓
交于
兩點，點
為橢圓
的左焦點．
（Ⅰ）求橢圓的離心率及左焦點的坐標；
（Ⅱ）求證：直線
與橢圓相切；
（Ⅲ）判斷
是否為定值，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中正確命題的序號是（ ）
①函數f（x）在定義域R內可導，“f′（1）＝0”是“函數f（x）在x＝1處取極值”的充分不必要條件；
②函數f（x）＝x3
ax在[1，2]上單調遞增，則a≥﹣4
③在一次射箭比賽中，甲、乙兩名射箭手各射箭一次．設命題p：“甲射中十環”，命題q：“乙射中十環”，則命題“至少有一名射箭手沒有射中十環”可表示為（￢p）∨（￢q）；
④若橢圓
左、右焦點分別為F1，F2，垂直于x軸的直線交橢圓于A，B兩點，當直線過右焦點時，△ABF1的周長取最大值
A.①③④B.②③④C.②③D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
