已知點p是圓(x+1)2+y2=16上的動點,圓心為B.A(1,0)是圓內的定點;PA的中垂線交BP于點Q.
(1)求點Q的軌跡C的方程;
(2)若直線l交軌跡C于M,N(MN與x軸、y軸都不平行)兩點,G為MN的中點,求KMN•KOG的值(O為坐標系原點).
【答案】
分析:(1)利用垂直平分線的性質可得|QA|=|QP|,由|QB|+|QP|=4,可得|QB|+|QA|=4,利用橢圓的定義可得點Q的軌跡是一個橢圓;
(2)法一:設M(x
1,y
1),N(x
2,y
2)(x
1≠x
2,y
1≠y
2),則
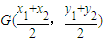
.代入可得
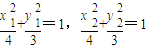
,利用點差法可得
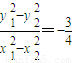
.再利用斜率計算公式即可得出K
MN•K
OG的值;
法二:設M(x
1,y
1),N(x
2,y
2)(x
1≠x
2,y
1≠y
2),直線MN的方程為y=kx+b(k≠0),則
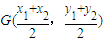
,
由于y
1=kx
1+b,y
2=kx
2+b,可得y
1+y
2=k(x
1+x
2)+2b,利用斜率計算公式可得
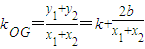
,將y=kx+b代入橢圓方程得:(4k
2+3)x
2+8kbx+4b
2-12=0,利用根與系數的關系可得
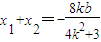
,代入得到
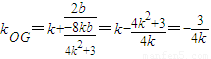
,即可得出K
MN•K
OG的值.
解答:解:(1)由條件知:|QA|=|QP|,
∵|QB|+|QP|=4,
∴|QB|+|QA|=4,
∵|AB|=2<4,
所以點Q的軌跡是以B,A為焦點的橢圓,
∵2a=4,2c=2,∴b
2=3,
所以點Q的軌跡C的方程是
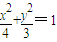
.
(2)設M(x
1,y
1),N(x
2,y
2)(x
1≠x
2,y
1≠y
2),則
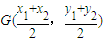
.
∵直線l與橢圓相較于點M,N,
∴
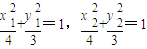
,
∴
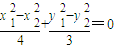
,可得
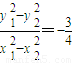
.
∵
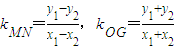
,
∴
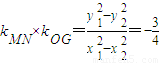
.
另解:設M(x
1,y
1),N(x
2,y
2)(x
1≠x
2,y
1≠y
2),直線MN的方程為y=kx+b(k≠0),
則
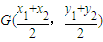
,
∵y
1=kx
1+b,y
2=kx
2+b,∴y
1+y
2=k(x
1+x
2)+2b,
∴
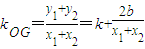
,
將y=kx+b代入橢圓方程得:(4k
2+3)x
2+8kbx+4b
2-12=0,
∴
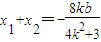
,
∴
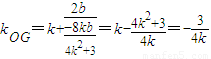
,
所以
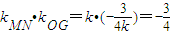
.
點評:本題綜合考查了圓與橢圓的定義及其標準方程、線段的垂直平分線、直線與橢圓相交問題轉化為根與系數的關系、直線的斜率計算公式、點差法等基礎知識與基本技能,考查了數形結合的能力、推理能力、計算能力.

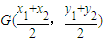 .代入可得
.代入可得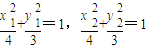 ,利用點差法可得
,利用點差法可得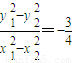 .再利用斜率計算公式即可得出KMN•KOG的值;
.再利用斜率計算公式即可得出KMN•KOG的值;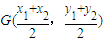 ,
,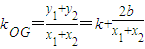 ,將y=kx+b代入橢圓方程得:(4k2+3)x2+8kbx+4b2-12=0,利用根與系數的關系可得
,將y=kx+b代入橢圓方程得:(4k2+3)x2+8kbx+4b2-12=0,利用根與系數的關系可得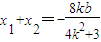 ,代入得到
,代入得到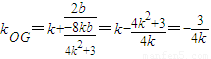 ,即可得出KMN•KOG的值.
,即可得出KMN•KOG的值.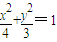 .
.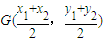 .
.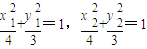 ,
,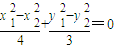 ,可得
,可得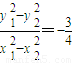 .
.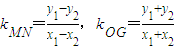 ,
,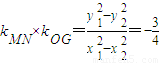 .
.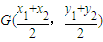 ,
,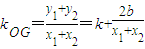 ,
,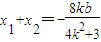 ,
,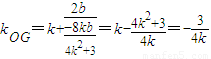 ,
,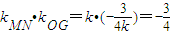 .
.

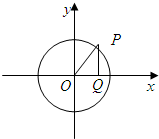 已知點P是圓x2+y2=1上的一個動點,過點P作PQ⊥x軸于點Q,設
已知點P是圓x2+y2=1上的一個動點,過點P作PQ⊥x軸于點Q,設