
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在
在![]() 處的切線(xiàn)方程;
處的切線(xiàn)方程;
(2)當(dāng)![]() 時(shí)恒有
時(shí)恒有![]() 成立,求滿(mǎn)足條件的m的范圍;
成立,求滿(mǎn)足條件的m的范圍;
(3)當(dāng)![]() 時(shí),令方程
時(shí),令方程![]() 有兩個(gè)不同的根
有兩個(gè)不同的根![]() ,
,![]() ,且滿(mǎn)足
,且滿(mǎn)足![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() (3)證明見(jiàn)解析.
(3)證明見(jiàn)解析.
【解析】
(1)求出![]() 和
和![]() 即可
即可
(2)由![]() ,
,![]() 得
得![]() ,即
,即![]()
(3)先利用導(dǎo)數(shù)得出![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,其中
上單調(diào)遞增,其中![]() ,然后分別求出
,然后分別求出![]() 在
在![]() 處的切線(xiàn)方程和
處的切線(xiàn)方程和![]() 在
在![]() 處的切線(xiàn),然后結(jié)合圖象即可證明.
處的切線(xiàn),然后結(jié)合圖象即可證明.
(1)由題意,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() .
.
![]() .
.
∵![]() .
.
∴函數(shù)![]() 在
在![]() 處的切線(xiàn)方程為:
處的切線(xiàn)方程為:![]() .
.
(2)由題意,當(dāng)![]() 時(shí)恒有
時(shí)恒有![]() 成立,
成立,
即![]() 對(duì)任意
對(duì)任意![]() 成立.
成立.
∵當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,
恒成立,
∴![]() 對(duì)任意
對(duì)任意![]() 恒成立.
恒成立.
∴![]() .
.
∴m的取值范圍為![]() .
.
(3)證明:由題意,當(dāng)![]() 時(shí),
時(shí),![]() .
.
![]() .
.
①令![]() ,即
,即![]() ,
,
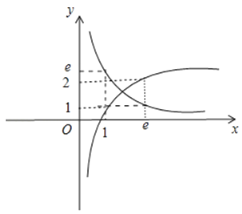
根據(jù)圖,很明顯交點(diǎn)的橫坐標(biāo)在1與![]() 之間,設(shè)為
之間,設(shè)為![]() ,
,
即![]() 的解為
的解為![]() ,(
,(![]() ),且
),且![]() .
.
②令![]() ,即
,即![]() x,解得
x,解得![]() ;
;
③令![]() ,即
,即![]() ,解得
,解得![]() .
.
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 處取得極小值.
處取得極小值.
∵![]() ,
,![]() .
.
∴根據(jù)題意,畫(huà)圖如下:

由圖,①設(shè)函數(shù)![]() 在
在![]() 處的切線(xiàn)為
處的切線(xiàn)為![]() ,
,
∵![]() .
.
∴直線(xiàn)![]() 的直線(xiàn)方程:
的直線(xiàn)方程:![]() ,
,
令![]() ,解得
,解得![]() ;
;
②設(shè)函數(shù)![]() 在
在![]() 處的切線(xiàn)為
處的切線(xiàn)為![]() ,
,
∵![]() .∴直線(xiàn)
.∴直線(xiàn)![]() 的直線(xiàn)方程:
的直線(xiàn)方程:![]() ,
,
令![]() ,解得
,解得![]() .
.
∴![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】波羅尼斯(古希臘數(shù)學(xué)家,的公元前262-190年)的著作《圓錐曲線(xiàn)論》是古代世界光輝的科學(xué)成果,它將圓錐曲線(xiàn)的性質(zhì)網(wǎng)羅殆盡,幾乎使后人沒(méi)有插足的余地.他證明過(guò)這樣一個(gè)命題:平面內(nèi)與兩定點(diǎn)距離的比為常數(shù)k(k>0,且k≠1)的點(diǎn)的軌跡是圓,后人將這個(gè)圓稱(chēng)為阿波羅尼斯圓.現(xiàn)有橢圓![]() =1(a>b>0),A,B為橢圓的長(zhǎng)軸端點(diǎn),C,D為橢圓的短軸端點(diǎn),動(dòng)點(diǎn)M滿(mǎn)足
=1(a>b>0),A,B為橢圓的長(zhǎng)軸端點(diǎn),C,D為橢圓的短軸端點(diǎn),動(dòng)點(diǎn)M滿(mǎn)足![]() =2,△MAB面積的最大值為8,△MCD面積的最小值為1,則橢圓的離心率為( )
=2,△MAB面積的最大值為8,△MCD面積的最小值為1,則橢圓的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地區(qū)現(xiàn)有一個(gè)直角梯形水產(chǎn)養(yǎng)殖區(qū)ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在點(diǎn)P處有一燈塔(如圖),且點(diǎn)P到BC,CD的距離都是1200m,現(xiàn)擬將養(yǎng)殖區(qū)ACD分成兩塊,經(jīng)過(guò)燈塔P增加一道分隔網(wǎng)EF,在△AEF內(nèi)試驗(yàn)養(yǎng)殖一種新的水產(chǎn)品,當(dāng)△AEF的面積最小時(shí),對(duì)原有水產(chǎn)品養(yǎng)殖的影響最小.設(shè)AE=d.
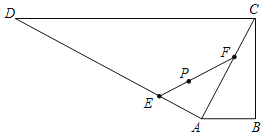
(1)若P是EF的中點(diǎn),求d的值;
(2)求對(duì)原有水產(chǎn)品養(yǎng)殖的影響最小時(shí)的d的值,并求△AEF面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在邊長(zhǎng)為4的正方形![]() 中,
中,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 是
是![]() 的中點(diǎn),現(xiàn)將三角形
的中點(diǎn),現(xiàn)將三角形![]() 沿
沿![]() 翻折成如圖2所示的五棱錐
翻折成如圖2所示的五棱錐![]() .
.
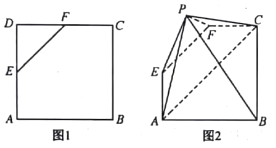
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直線(xiàn)
,求直線(xiàn)![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三個(gè)元素,分別作為一個(gè)三位數(shù)的個(gè)位數(shù),十位數(shù)和百位數(shù),記這個(gè)三位數(shù)為a,現(xiàn)將組成a的三個(gè)數(shù)字按從小到大排成的三位數(shù)記為I(a),按從大到小排成的三位數(shù)記為D(a)(例如a=219,則I(a)=129,D(a)=921),閱讀如圖所示的程序框圖,運(yùn)行相應(yīng)的程序,任意輸入一個(gè)a,則輸出b的值為( )
A. 792 B. 693 C. 594 D. 495
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線(xiàn)
中,直線(xiàn)![]() 的傾斜角為
的傾斜角為![]() ,且經(jīng)過(guò)點(diǎn)
,且經(jīng)過(guò)點(diǎn)![]() .以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,直線(xiàn)
.以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,直線(xiàn)![]() ,從原點(diǎn)O作射線(xiàn)交
,從原點(diǎn)O作射線(xiàn)交![]() 于點(diǎn)M,點(diǎn)N為射線(xiàn)OM上的點(diǎn),滿(mǎn)足
于點(diǎn)M,點(diǎn)N為射線(xiàn)OM上的點(diǎn),滿(mǎn)足![]() ,記點(diǎn)N的軌跡為曲線(xiàn)C.
,記點(diǎn)N的軌跡為曲線(xiàn)C.
(Ⅰ)求出直線(xiàn)![]() 的參數(shù)方程和曲線(xiàn)C的直角坐標(biāo)方程;
的參數(shù)方程和曲線(xiàn)C的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線(xiàn)![]() 與曲線(xiàn)C交于P,Q兩點(diǎn),求
與曲線(xiàn)C交于P,Q兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線(xiàn)![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,以極點(diǎn)為原點(diǎn),極軸為
,以極點(diǎn)為原點(diǎn),極軸為![]() 軸的正半軸,建立平面直角坐標(biāo)系,直線(xiàn)
軸的正半軸,建立平面直角坐標(biāo)系,直線(xiàn)![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,傾斜角為
,傾斜角為![]() .
.
(1)求曲線(xiàn)![]() 的直角坐標(biāo)方程與直線(xiàn)l的參數(shù)方程;
的直角坐標(biāo)方程與直線(xiàn)l的參數(shù)方程;
(2)設(shè)直線(xiàn)![]() 與曲線(xiàn)
與曲線(xiàn)![]() 交于
交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=x-lnx,g(x)=x2-ax.
(1)求函數(shù)f(x)在區(qū)間[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函數(shù)h(x)圖像上任意兩點(diǎn),且滿(mǎn)足![]() >1,求實(shí)數(shù)a的取值范圍;
>1,求實(shí)數(shù)a的取值范圍;
(3)若x∈(0,1],使f(x)≥![]() 成立,求實(shí)數(shù)a的最大值.
成立,求實(shí)數(shù)a的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點(diǎn),
上的點(diǎn),![]() 的面積最大值為
的面積最大值為![]() ,直線(xiàn)
,直線(xiàn)![]() 與
與![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() (
(![]() 為坐標(biāo)原點(diǎn))
為坐標(biāo)原點(diǎn))
(1)求橢圓![]() 的方程;
的方程;
(2)求證:![]() 到直線(xiàn)
到直線(xiàn)![]() 的距離為定值,并求其定值.
的距離為定值,并求其定值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com