欧美成人一区二区,国产成人精品无人区一区,国产精品久久久久久久久久小说

精英家教網 > 高中數學 > 題目詳情

【題目】設，在復平面內對應點Z，試說明滿足下列條件的點Z的集合是什么圖形．

（1）；

（2）．

【答案】（1）以原點O為圓心，2為半徑的圓．

（2）原點O為圓心，以1和2為半徑的兩圓所夾的圓環，并且包括圓環的邊界

【解析】

（1）根據復數模的定義確定復數對應點滿足條件，即得軌跡；

（2）根據復數模的定義確定復數對應點滿足條件，即得軌跡.

解：（1）方法一說明復數z在復平面內對應的點Z到原點的距離為2，這樣的點Z的集合是以原點O為圓心，2為半徑的圓．

方法二設，由，得．

故點Z對應的集合是以原點O為圓心，2為半徑的圓．

（2）不等式可以轉化為不等式組

不等式的解集是圓及該圓內部所有點的集合．

不等式的解集是圓及該圓外部所有點的集合．

這兩個集合的交集，就是滿足條件的點的集合．

如圖中的陰影部分，

所求點的集合是以原點O為圓心，以1和2為半徑的兩圓所夾的圓環，并且包括圓環的邊界．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

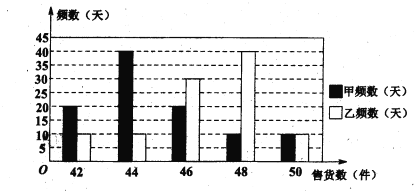
【題目】甲、乙兩家銷售公司擬各招聘一名產品推銷員，日工資方案如下: 甲公司規定底薪80元，每銷售一件產品提成1元; 乙公司規定底薪120元，日銷售量不超過45件沒有提成，超過45件的部分每件提成8元.

(I)請將兩家公司各一名推銷員的日工資 (單位: 元) 分別表示為日銷售件數的函數關系式;

(II)從兩家公司各隨機選取一名推銷員，對他們過去100天的銷售情況進行統計，得到如下條形圖。若記甲公司該推銷員的日工資為,乙公司該推銷員的日工資為 (單位: 元)，將該頻率視為概率，請回答下面問題:

某大學畢業生擬到兩家公司中的一家應聘推銷員工作，如果僅從日均收入的角度考慮，請你利用所學的統計學知識為他作出選擇，并說明理由.

【答案】(I)見解析； (Ⅱ)見解析.

【解析】分析：(I)依題意可得甲公司一名推銷員的工資與銷售件數的關系是一次函數的關系式，而乙公司是分段函數的關系式，由此解得；(Ⅱ)分別根據條形圖求得甲、乙公司一名推銷員的日工資的分布列，從而可分別求得數學期望，進而可得結論.

詳解：(I)由題意得,甲公司一名推銷員的日工資 (單位:元) 與銷售件數的關系式為: .

乙公司一名推銷員的日工資 (單位: 元) 與銷售件數的關系式為:

(Ⅱ)記甲公司一名推銷員的日工資為 (單位: 元),由條形圖可得的分布列為

	122	124	126	128	130
	0.2	0.4	0.2	0.1	0.1

記乙公司一名推銷員的日工資為 (單位: 元),由條形圖可得的分布列為

	120	128	144	160
	0.2	0.3	0.4	0.1

∴

∴僅從日均收入的角度考慮，我會選擇去乙公司.

點睛：求解離散型隨機變量的數學期望的一般步驟為：

第一步是“判斷取值”，即判斷隨機變量的所有可能取值，以及取每個值所表示的意義；

第二步是“探求概率”，即利用排列組合，枚舉法，概率公式，求出隨機變量取每個值時的概率；

第三步是“寫分布列”，即按規范形式寫出分布列，并注意用分布列的性質檢驗所求的分布列或某事件的概率是否正確；

第四步是“求期望值”，一般利用離散型隨機變量的數學期望的定義求期望的值

【題型】解答題
【結束】
19

【題目】如圖，在四棱錐中，底面為菱形，平面，，，，分別是，的中點.

（1）證明：；

（2）設為線段上的動點，若線段長的最小值為，求二面角的余弦值.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系，他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數，得到如表資料：

日期	1月10日	2月10日	3月10日	4月10日	5月10日	6月10日
晝夜溫差x（°C）	10	11	13	12	8	6
就診人數y（個）	22	25	29	26	16	12

該興趣小組確定的研究方案是：先從這六組數據中選取2組，用剩下的4組數據求線性回歸方程，再用被選取的2組數據進行檢驗．

（1）求選取的2組數據恰好是相鄰兩個月的概率；

（2）若選取的是1月與6月的兩組數據，請根據2至5月份的數據，求出關于的線性回歸方程；

（3）若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人，則認為得到的線性回歸方程是理想的，試問（2）中所得線性回歸方程是否理想?

參考公式：，

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】從全校參加數學競賽的學生的試卷中抽取一個樣本，考察競賽的成績分布情況，將樣本分成5組，繪成頻率分布直方圖，圖中從左到右各小長方形的高之比為，最右邊一組頻數是6，請結合直方圖提供的信息，解答下列問題：

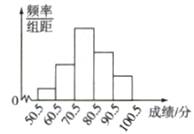
（1）樣本量是多少？

（2）列出頻率分布表.

（3）估計這次競賽中，成績高于60分的學生占總人數的百分比.

（4）成績落在哪個范圍內的人數最多？

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在直角坐標系中，點，曲線（為參數），其中，在以為極點，軸正半軸為極軸的極坐標系中，曲線：．

（Ⅰ）若，求與公共點的直角坐標；

（Ⅱ）若與相交于不同的兩點，是線段的中點，當時，求的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】物聯網（Internet of Things，縮寫：IOT）是基于互聯網、傳統電信網等信息承載體，讓所有能行使獨立功能的普通物體實現互聯互通的網絡. 其應用領域主要包括運輸和物流、工業制造、健康醫療、智能環境（家庭、辦公、工廠）等，具有十分廣闊的市場前景. 現有一家物流公司計劃租地建造倉庫儲存貨物，經過市場調查了解到下列信息：倉庫每月土地占地費（單位：萬元），倉庫到車站的距離（單位：千米，），其中與成反比，每月庫存貨物費（單位：萬元）與成正比;若在距離車站9千米處建倉庫，則和分別為2萬元和7. 2萬元. 這家公司應該把倉庫建在距離車站多少千米處，才能使兩項費用之和最小？最小費用是多少？