
已知函數 ,數列
,數列 滿足
滿足 ,且
,且 .
.
(1)試探究數列 是否是等比數列?
是否是等比數列?
(2)試證明 ;
;
(3)設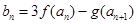 ,試探究數列
,試探究數列 是否存在最大項和最小項?若存在求出
是否存在最大項和最小項?若存在求出
最大項和最小項,若不存在,說明理由.
 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com