
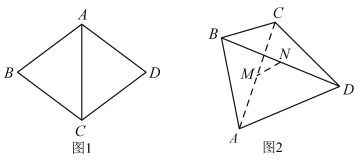
【題目】如圖1.四邊形![]() 是邊長為10的菱形,其對角線
是邊長為10的菱形,其對角線![]() ,現將
,現將![]() 沿對角線
沿對角線![]() 折起,連接
折起,連接![]() ,形成如圖2的四面體
,形成如圖2的四面體![]() ,則異面直線
,則異面直線![]() 與
與![]() 所成角的大小為______.在圖2中,設棱
所成角的大小為______.在圖2中,設棱![]() 的中點為
的中點為![]() ,
,![]() 的中點為
的中點為![]() ,若四面體
,若四面體![]() 的外接球的球心在四面體的內部,則線段
的外接球的球心在四面體的內部,則線段![]() 長度的取值范圍為______.
長度的取值范圍為______.
【答案】![]()
![]()
【解析】
連接![]() 、
、![]() ,利用線面垂直的判定定理可求異面直線
,利用線面垂直的判定定理可求異面直線![]() 與
與![]() 所成角的大小;先根據外接球的性質確定出四面體
所成角的大小;先根據外接球的性質確定出四面體![]() 的外接球球心,利用勾股定理,求出
的外接球球心,利用勾股定理,求出![]() 和
和![]() ,進而求出
,進而求出![]() ,借助三角函數的取值范圍以及
,借助三角函數的取值范圍以及![]() ,即可求出線段
,即可求出線段![]() 長度的取值范圍.
長度的取值范圍.
連接![]() 、
、![]() ,四邊形
,四邊形![]() 是菱形,
是菱形,![]() 為棱
為棱![]() 的中點,
的中點,
所以![]() ,
,![]() ,
,
又![]() ,
,
則![]() 平面
平面![]() ,
,
由![]() 平面
平面![]() ,
,
則![]() ,即異面直線
,即異面直線![]() 與
與![]() 所成角的大小為
所成角的大小為![]() .
.
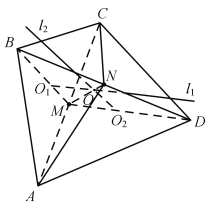
由四邊形![]() 是邊長為10的菱形,其對角線
是邊長為10的菱形,其對角線![]() ,
,
則![]() ,
,![]() ,
,
![]() 是
是![]() 的外心,在中線
的外心,在中線![]() 中,
中,
設過點![]() 的直線
的直線![]() 平面
平面![]() ,易知
,易知![]() 平面
平面![]() ,
,
同理![]() 是
是![]() 的外心,在中線
的外心,在中線![]() 上,
上,
設過點![]() 的直線
的直線![]() 平面
平面![]() ,易知
,易知![]() 平面
平面![]() ,
,
由對稱性易知![]() 、
、![]() 的交點
的交點![]() 在直線
在直線![]() 上,
上,
根據外接球的性質,點![]() 為四面體
為四面體![]() 的外接球的球心,
的外接球的球心,
![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
令![]() ,根據題意可知
,根據題意可知![]() ,
,![]() ,且
,且![]() ,
,
則![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,則
,則![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() ,即線段
,即線段![]() 長度的取值范圍為
長度的取值范圍為![]() ,
,
故答案為:![]() ;
;![]()


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】在四面體ABCD中,△ABC和△BCD均是邊長為1的等邊三角形,已知四面體ABCD的四個頂點都在同一球面上,且AD是該球的直徑,則四面體ABCD的體積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市先后采用甲、乙兩種方案治理空氣污染各一年,各自隨機抽取一年(365天)內100天的空氣質量指數API的檢測數據進行分析,若空氣質量指數值在[0,300]內為合格,否則為不合格.表1是甲方案檢測數據樣本的頻數分布表,如圖是乙方案檢測數據樣本的頻率分布直方圖.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天數 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
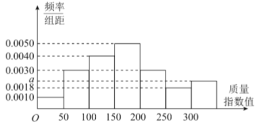
(1)將頻率視為概率,求乙方案樣本的頻率分布直方圖中![]() 的值,以及乙方案樣本的空氣質量不合格天數;
的值,以及乙方案樣本的空氣質量不合格天數;
(2)求乙方案樣木的中位數;
(3)填寫下面2×2列聯表(如表2),并根據列聯表判斷是否有90%的把握認為該城市的空氣質量指數值與兩種方案的選擇有關.
表2:
甲方案 | 乙方案 | 合計 | |
合格天數 | _______ | _______ | _______ |
不合格天數 | _______ | _______ | _______ |
合計 | _______ | _______ | _______ |
附: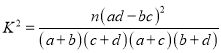
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的離心率是
的離心率是![]() ,一個頂點是
,一個頂點是![]() .
.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() ,
,![]() 是橢圓
是橢圓![]() 上異于點
上異于點![]() 的任意兩點,且
的任意兩點,且![]() .試問:直線
.試問:直線![]() 是否恒過一定點?若是,求出該定點的坐標;若不是,說明理由.
是否恒過一定點?若是,求出該定點的坐標;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的離心率為
的離心率為![]() ,雙曲線
,雙曲線![]() 的漸近線與橢圓
的漸近線與橢圓![]() 的交點到原點的距離均為
的交點到原點的距離均為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若點![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 三點共線,直線
三點共線,直線![]() 的斜率分別為
的斜率分別為![]() .
.
(i)證明:![]() ;
;
(ii)若![]() ,設直線
,設直線![]() 過點
過點![]() ,直線
,直線![]() 過點
過點![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是數列1,
是數列1,![]() ,
,![]() ,…,
,…,![]() 的各項和,
的各項和,![]() ,
,![]() .
.
(1)設![]() ,證明:
,證明:![]() 在
在![]() 內有且只有一個零點;
內有且只有一個零點;
(2)當![]() 時,設存在一個與上述數列的首項、項數、末項都相同的等差數列,其各項和為
時,設存在一個與上述數列的首項、項數、末項都相同的等差數列,其各項和為![]() ,比較
,比較![]() 與
與![]() 的大小,并說明理由;
的大小,并說明理由;
(3)給出由公式![]() 推導出公式
推導出公式![]() 的一種方法如下:在公式
的一種方法如下:在公式![]() 中兩邊求導得:
中兩邊求導得:![]() ,所以
,所以![]() 成立,請類比該方法,利用上述數列的末項
成立,請類比該方法,利用上述數列的末項![]() 的二項展開式證明:
的二項展開式證明:![]() 時
時![]() (其中
(其中![]() 表示組合數)
表示組合數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為提高產品質量,某企業質量管理部門經常不定期地對產品進行抽查檢測,現對某條生產線上隨機抽取的100個產品進行相關數據的對比,并對每個產品進行綜合評分(滿分100分),將每個產品所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為80分及以上的產品為一等品.
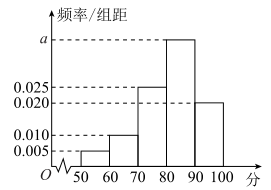
(1)求圖中![]() 的值,并求綜合評分的中位數;
的值,并求綜合評分的中位數;
(2)用樣本估計總體,視頻率作為概率,在該條生產線中隨機抽取3個產品,求所抽取的產品中一等品數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 是定義域為
是定義域為![]() 的奇函數,且它的最小正周期是T,已知
的奇函數,且它的最小正周期是T,已知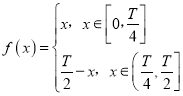 ,
,![]() .給出下列四個判斷:①對于給定的正整數
.給出下列四個判斷:①對于給定的正整數![]() ,存在
,存在![]() ,使得
,使得![]() 成立;②當a
成立;②當a![]() 時,對于給定的正整數
時,對于給定的正整數![]() ,存在
,存在![]() ,使得
,使得![]() 成立;③當
成立;③當![]()
![]() 時,函數
時,函數![]() 既有對稱軸又有對稱中心;④當
既有對稱軸又有對稱中心;④當![]()
![]() 時,
時,![]() 的值只有0或
的值只有0或![]() .其中正確判斷的有( )
.其中正確判斷的有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com