
【題目】如圖,某學校準備修建一個面積為2400平方米的矩形活動場地(圖中ABCD)的圍欄,按照修建要求,中間用圍墻EF隔開,使得ABEF為矩形,EFCD為正方形,設![]() 米,已知圍墻(包括EF)的修建費用均為每米500元,設圍墻(包括EF)的修建總費用為y元.
米,已知圍墻(包括EF)的修建費用均為每米500元,設圍墻(包括EF)的修建總費用為y元.
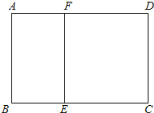
(1)求出y關于x的函數解析式及x的取值范圍;
(2)當x為何值時,圍墻(包括EF)的修建總費用y最小?并求出y的最小值.
【答案】(1)![]()
![]() ;(2)當
;(2)當![]() 為20米時,
為20米時,![]() 最小.
最小.![]() 的最小值為96000元.
的最小值為96000元.
【解析】
試題(1)由題意,已知了整個矩形場地的面積,又設了寬AB為x米,所以其長就應為![]() 米,從而圍墻的長度就為:(
米,從而圍墻的長度就為:(![]() )米,從而修建總費用
)米,從而修建總費用![]() 元,只是注意求函數的解析式一定要指出函數的定義域,此題中不僅要
元,只是注意求函數的解析式一定要指出函數的定義域,此題中不僅要![]() 而且還要注意題目中的隱含條件:“中間用圍墻
而且還要注意題目中的隱含條件:“中間用圍墻![]() 隔開,使得
隔開,使得![]() 為矩形,
為矩形,![]() 為正方形”從而可知矩形ABCD的長
為正方形”從而可知矩形ABCD的長![]() 應當要大于其寬x,所以x還應滿足:
應當要大于其寬x,所以x還應滿足:![]() ;(2)由(1)知
;(2)由(1)知![]() 所以可用基本不等式來求y的最小值,及對應的x的值;最后應用問題一定要注意將數學解得的結果還原成實際問題的結果.
所以可用基本不等式來求y的最小值,及對應的x的值;最后應用問題一定要注意將數學解得的結果還原成實際問題的結果.
試題解析:(1)設![]() 米,則由題意得
米,則由題意得![]() ,且
,且![]() 2分
2分
故![]() ,可得
,可得![]() 4分
4分
(說明:若缺少“![]() ”扣2分)
”扣2分)
則![]() , 6分
, 6分
所以![]() 關于
關于![]() 的函數解析式為
的函數解析式為![]()
![]() . 7分
. 7分
(2)![]() , 10分
, 10分
當且僅當![]() ,即
,即![]() 時等號成立. 12分
時等號成立. 12分
故當![]() 為20米時,
為20米時,![]() 最小.
最小.![]() 的最小值為96000元. 14分
的最小值為96000元. 14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩種坐標系中的長度單位相同,已知曲線
軸的正半軸,兩種坐標系中的長度單位相同,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)直線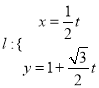 (
(![]() 為參數)與曲線
為參數)與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區有小學21所,中學14所,大學7所,現采取分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查。
(I)求應從小學、中學、大學中分別抽取的學校數目。
(II)若從抽取的6所學校中隨機抽取2所學校做進一步數據分析,
(1)列出所有可能的抽取結果;
(2)求抽取的2所學校均為小學的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的離心率為
的離心率為![]() ,過點A(0,-b)和B(a,0)的直線與原點的距離為
,過點A(0,-b)和B(a,0)的直線與原點的距離為![]() .
.
(1)求雙曲線C的方程;
(2)直線y=kx+m(k≠0, m≠0)與該雙曲線C交于不同的兩點C,D,且C,D兩點都在以點A為圓心的同一圓上,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)的二次項系數為a(a<0).1,3是函數y=f(x)+2x的兩個零點.若方程f(x)+6a=0有兩個相等的根,求f(x)的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為回饋顧客,某商場擬通過摸球兌獎的方式對1000位顧客進行獎勵,規定:每位顧客從一個裝有4個標有面值的球的袋中一次性隨機摸出2個球,球上所標的面值之和為該顧客所獲的獎勵額.
(1)若袋中所裝的4個球中有1個所標的面值為50元,其余3個均為10元,求:
①顧客所獲的獎勵額為60元的概率;
②顧客所獲的獎勵額的分布列及數學期望;
(2)商場對獎勵總額的預算是60000元,并規定袋中的4個球只能由標有面值10元和50元的兩種球組成,或標有面值20元和40元的兩種球組成.為了使顧客得到的獎勵總額盡可能符合商場的預算且每位顧客所獲的獎勵額相對均衡,請對袋中的4個球的面值給出一個合適的設計,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 市某機構為了調查該市市民對我國申辦
市某機構為了調查該市市民對我國申辦![]() 年足球世界杯的態度,隨機選取了
年足球世界杯的態度,隨機選取了![]() 位市民進行調查,調查結果統計如下:
位市民進行調查,調查結果統計如下:
支持 | 不支持 | 總計 | |
男性市民 |
| ||
女性市民 |
| ||
總計 |
|
|
(1)根據已知數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過![]() 的前提下認為支持申辦
的前提下認為支持申辦![]() 年足球世界杯與性別有關?請說明理由.
年足球世界杯與性別有關?請說明理由.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com