
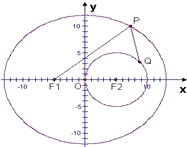
 已知點P是橢圓
已知點P是橢圓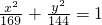 上一動點,點F1,F2是橢圓的左右兩焦點.
上一動點,點F1,F2是橢圓的左右兩焦點.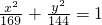
 …(4分)
…(4分) p=
p=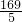 ,p=
,p= =67.6
=67.6 )
) r2r1sin30°=144(2-
r2r1sin30°=144(2- )…(13分)
)…(13分)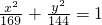 的標準方程得出a=13,b=12,c=5,從而得到長軸長26,右準線方x=
的標準方程得出a=13,b=12,c=5,從而得到長軸長26,右準線方x=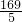 ;
; p=
p=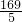 ,p=
,p= =135.2,最后寫出拋物線標準方程;
=135.2,最后寫出拋物線標準方程; ),根據面積公式即可求得△PF1F2的面積;
),根據面積公式即可求得△PF1F2的面積;

科目:高中數學 來源: 題型:
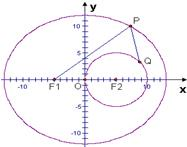 已知點P是橢圓
已知點P是橢圓| x2 |
| 169 |
| y2 |
| 144 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| MA |
| MB |
| AB |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年重慶市主城八區高三第二次調研數學試卷(理科)(解析版) 題型:解答題
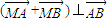 的實數m的取值范圍.
的實數m的取值范圍.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com