
【題目】如圖,已知正三棱錐P-ABC的側面是直角三角形,PA=6,頂點P在平面ABC內的正投影為點D,D在平面PAB內的正投影為點E,連結PE并延長交AB于點G.

(Ⅰ)證明:G是AB的中點;
(Ⅱ)在圖中作出點E在平面PAC內的正投影F(說明作法及理由),并求四面體PDEF的體積.
【答案】(Ⅰ)見解析;(Ⅱ)作圖見解析,體積為![]() .
.
【解析】試題分析:證明![]() 由
由![]() 可得
可得![]() 是
是![]() 的中點.(Ⅱ)在平面
的中點.(Ⅱ)在平面![]() 內,過點
內,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() ,
, ![]() 即為
即為![]() 在平面
在平面![]() 內的正投影.根據正三棱錐的側面是直角三角形且
內的正投影.根據正三棱錐的側面是直角三角形且![]() ,可得
,可得![]() 在等腰直角三角形
在等腰直角三角形![]() 中,可得
中,可得![]() 四面體
四面體![]() 的體積
的體積![]()
試題解析:(Ⅰ)因為![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,所以
,所以![]()
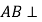
因為![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,所以
,所以![]()
所以![]() 平面
平面![]() ,故
,故![]()
又由已知可得, ![]() ,從而
,從而![]() 是
是![]() 的中點.
的中點.
(Ⅱ)在平面![]() 內,過點
內,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() ,
, ![]() 即為
即為![]() 在平面
在平面![]() 內的正投影.
內的正投影.
理由如下:由已知可得![]()
![]() ,
, ![]() ,又
,又![]() ,所以
,所以![]() ,因此
,因此![]() 平面
平面![]() ,即點
,即點![]() 為
為![]() 在平面
在平面![]() 內的正投影.
內的正投影.
連結![]() ,因為
,因為![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,所以
,所以![]() 是正三角形
是正三角形![]() 的中心.
的中心.
由(Ⅰ)知, ![]() 是
是![]() 的中點,所以
的中點,所以![]() 在
在![]() 上,故
上,故![]()
由題設可得![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,因此
,因此![]()
由已知,正三棱錐的側面是直角三角形且![]() ,可得
,可得![]()
在等腰直角三角形![]() 中,可得
中,可得![]()
所以四面體![]() 的體積
的體積![]()


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】為了保證食品的安全衛生,食品監督管理部門對某食品廠生產甲、乙兩種食品進行了檢測調研,檢測某種有害微量元素的含量,隨機在兩種食品中各抽取了10個批次的食品,每個批次各隨機地抽取了一件,下表是測量數據的莖葉圖(單位:毫克).規定:當食品中的有害微量元素的含量在![]() 時為一等品,在
時為一等品,在![]() 為二等品,20以上為劣質品.
為二等品,20以上為劣質品.

(1)用分層抽樣的方法在兩組數據中各抽取5個數據,再分別從這5個數據中各選取2個,求抽到食品甲包含劣質品的概率和抽到食品乙全是一等品的概率;
(2)在概率和統計學中,數學期望(或均值)是基本的統計概念,它反映隨機變量取值的平均水平.變量的一切可能的取值![]() 與對應的概率
與對應的概率![]() 乘積之和稱為該變量的數學期望,記為
乘積之和稱為該變量的數學期望,記為![]() .
.
參考公式:變量![]() 的取值為
的取值為![]() ,
,![]() 對應取值的概率
對應取值的概率![]() ,可理解為數據
,可理解為數據![]() 出現的頻率
出現的頻率![]() ,
,
![]()
![]() .
.
①每生產一件一等品盈利50元,二等品盈利20元,劣質品虧損20元,根據上表統計得到甲、乙兩種食品為一等品、二等品、劣質品的頻率,分別估計這兩種食品為一等品、 二等品、劣質品的概率,若分別從甲、乙食品中各抽取1件,求這兩件食品各自能給該廠 帶來的盈利期望![]() .
.
②若生產食品甲初期需要一次性投入10萬元,生產食品乙初期需要一次性投人16 萬元,但是以目前企業的狀況,甲乙兩條生產線只能投資其中一條.如果你是該食品廠負責人,以一年為期限,盈利為參照,請給出合理的投資方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),過原點的兩條直線
為參數),過原點的兩條直線![]() 分別與曲線
分別與曲線![]() 交于異于原點的
交于異于原點的![]() 、
、![]() 兩點,且
兩點,且![]() ,其中
,其中![]() 的傾斜角為
的傾斜角為![]() .以坐標原點為極點,
.以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求![]() 和
和![]() 的極坐標方程;
的極坐標方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() 的一個焦點與拋物線y2=-4x的焦點相同,且橢圓C上一點與橢圓C的左,右焦點F1,F2構成的三角形的周長為
的一個焦點與拋物線y2=-4x的焦點相同,且橢圓C上一點與橢圓C的左,右焦點F1,F2構成的三角形的周長為![]() .
.
(1)求橢圓C的方程;
(2)若直線l:y=kx+m(k,m∈R)與橢圓C交于A,B兩點,O為坐標原點,△AOB的重心G滿足: ![]() ,求實數m的取值范圍.
,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是![]() 的中點.
的中點.

(1)設P是![]() 上的一點,且AP⊥BE,求∠CBP的大小;
上的一點,且AP⊥BE,求∠CBP的大小;
(2)當AB=3,AD=2時,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分別是BC,BB1,A1D的中點.

(1)證明:MN∥平面C1DE;
(2)求點C到平面C1DE的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場對顧客實行購物優惠活動規定,一次購物付款總額:
(1)如果標價總額不超過200元,則不給予優惠;
(2)如果標價總額超過200元但不超過500元,則按標價總額給予9折優惠;
(3)如果標價總額超過500元,其500元內的按第(2)條給予優惠,超過500元的部分給予8折優惠.
某人兩次去購物,分別付款180元和423元,假設他一次性購買上述兩次同樣的商品,則應付款( )
A.550元B.560元C.570元D.580元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com