
【題目】已知函數![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 與曲線
與曲線![]() 的公切線的方程;
的公切線的方程;
(2)設函數![]() 的兩個極值點為
的兩個極值點為![]() ,求證:關于
,求證:關于![]() 的方程
的方程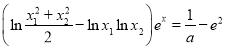 有唯一解.
有唯一解.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】
(1)求兩條曲線的公切線,分別求出各自的切線,然后兩條切線為同一條直線,結合兩個方程求解;
(2)要證明關于![]() 的方程
的方程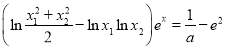 有唯一解,只要證明
有唯一解,只要證明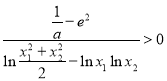 即可,由于當
即可,由于當![]() 時,
時,![]() 單調遞增,不可能有兩個零點,故
單調遞增,不可能有兩個零點,故![]() 不可能有兩個極值點,故
不可能有兩個極值點,故![]() ,利用
,利用![]() 得
得![]() ,又
,又![]()
![]() ,接下來只要證明
,接下來只要證明![]() ,即
,即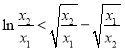 ,令
,令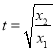 ,則只要證明
,則只要證明![]() 即可,用導數即可證明.
即可,用導數即可證明.
(1)曲線![]() 在切點
在切點![]() 處的切線方程為
處的切線方程為
![]() ,即
,即![]() ,
,
曲線![]() 在切點
在切點![]() 處的切線方程為
處的切線方程為
![]() ,即
,即![]() ,
,
由曲線![]() 與曲線
與曲線![]() 存在公切線,
存在公切線,
得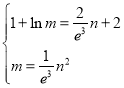 ,得
,得![]() ,即
,即![]() .
.
令![]() ,則
,則![]() ,
,
![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 上單調遞減,
上單調遞減,
又![]() ,∴
,∴![]() ,則
,則![]() ,
,
故公切線方程為![]() .
.
(2)要證明關于![]() 的方程
的方程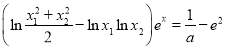 有唯一解,
有唯一解,
只要證明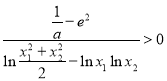 ,
,
先證明:![]() .
.
∵![]() 有兩個極值點,
有兩個極值點,
∴![]() 有兩個不同的零點,
有兩個不同的零點,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 恒成立,∴
恒成立,∴![]() 單調遞增,
單調遞增,![]() 不可能有兩個零點;
不可能有兩個零點;
當![]() 時,
時,![]() ,則
,則![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,則
,則![]() ,∴
,∴![]() 在
在![]() 上單調遞減,
上單調遞減,
又![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
∴![]() ,得
,得![]() ,∴
,∴![]() .
.
易知![]() ,
,
由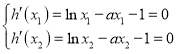 ,得
,得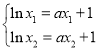 ,
,![]() ,
,
∴![]() .
.
下面再證明:![]() .
.
 ,
,
令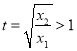 ,則只需證
,則只需證![]() ,
,
令![]() ,
,
則![]() ,
,
∴![]() ,得
,得![]() .
.
∴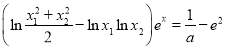 有唯一解.
有唯一解.


 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:
【題目】某流行病爆發期間,某市衛生防疫部門給出的治療方案中推薦了三種治療藥物![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 的使用是互斥且完備的),并且感染患者按規定都得到了藥物治療.患者在關于這三種藥物的有關參數及市場調查數據如下表所示:(表中的數據都以一個療程計)
的使用是互斥且完備的),并且感染患者按規定都得到了藥物治療.患者在關于這三種藥物的有關參數及市場調查數據如下表所示:(表中的數據都以一個療程計)
|
|
|
|
單價(單位:元) | 600 | 1000 | 800 |
治愈率 |
|
|
|
市場使用量(單位:人) | 305 | 122 | 183 |
(Ⅰ)從感染患者中任取一人,試求其一個療程被治愈的概率大約是多少?
(Ⅱ)試估算每名感染患者在一個療程的藥物治療費用平均是多少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,右焦點到右準線的距離為3.
,右焦點到右準線的距離為3.
(1)求橢圓C的標準方程;
(2)過點P(0,1)的直線l與橢圓C交于兩點A,B.己知在橢圓C上存在點Q,使得四邊形OAQB是平行四邊形,求Q的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() :
: ![]() 經過伸縮變換
經過伸縮變換![]() 后得到曲線
后得到曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求出曲線![]() 、
、![]() 的參數方程;
的參數方程;
(Ⅱ)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 、
、![]() 上的動點,求
上的動點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面多邊形![]() 中,
中,![]() 是邊長為2的正方形,
是邊長為2的正方形,![]() 為等腰梯形,
為等腰梯形,![]() 為
為![]() 的中點,且
的中點,且![]() ,
,![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折疊,使平面
折疊,使平面![]() 平面
平面![]() .
.
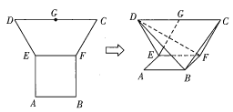
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在拋物線
在拋物線![]() 上,過點
上,過點![]() 的直線與拋物線交于A,B兩點,又過A,B兩點分作拋物線的切線,兩條切線交于P點.記直線PA、PB的斜率分別為
的直線與拋物線交于A,B兩點,又過A,B兩點分作拋物線的切線,兩條切線交于P點.記直線PA、PB的斜率分別為![]() 和
和![]() .
.
(1)求![]() 的值;
的值;
(2)![]() ,
,![]() ,求四邊形PAEG面積的最小值.
,求四邊形PAEG面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖平面PAC⊥平面ABC, AC⊥BC,PE// BC,M,N分別是AE,AP的中點,且△PAC是邊長為2的等邊三角形,BC=3,PE =2.

(1)求證:MN⊥平面PAC;
(2)求平面PAE與平面ABC夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解高三年級學生在線學習情況,統計了2020年2月18日-27日(共10天)他們在線學習人數及其增長比例數據,并制成如圖所示的條形圖與折線圖的組合圖.
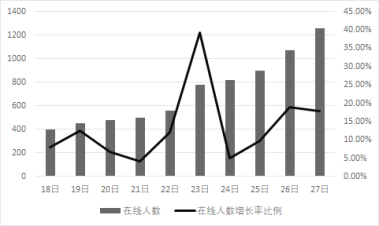
根據組合圖判斷,下列結論正確的是( )
A.前5天在線學習人數的方差大于后5天在線學習人數的方差
B.前5天在線學習人數的增長比例的極差大于后5天的在線學習人數的增長比例的極差
C.這10天學生在線學習人數的增長比例在逐日增大
D.這10天學生在線學習人數在逐日增加
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com