
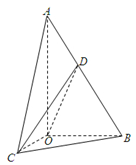
 如圖,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜邊AB=4.Rt△AOC可以通過Rt△AOB以直線AO為軸旋轉得到,且二面角B-AO-C是直二面角,動點D在斜邊AB上.
如圖,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜邊AB=4.Rt△AOC可以通過Rt△AOB以直線AO為軸旋轉得到,且二面角B-AO-C是直二面角,動點D在斜邊AB上.分析 (Ⅰ)由題意,CO⊥AO,BO⊥AO,∠BOC是二面角B-AO-C是直二面角,從而CO⊥BO,進而CO⊥平面AOB,由此能證明平面COD⊥平面AOB.
(Ⅱ)當VA-DOC:VA-BOC=1:2時,D為AB中點,以O為原點,OC為x軸,OB為y軸,OA為z軸,建立空間直角坐標系O-xyz,利用向量法能求出CD與平面AOB所成角.
解答 證明:(Ⅰ)由題意,CO⊥AO,BO⊥AO,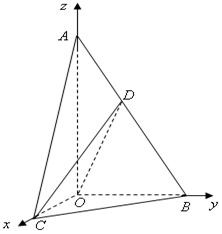
∴∠BOC是二面角B-AO-C是直二面角,
又∵二面角B-AO-C是直二面角,∴CO⊥BO,
又∵AO∩BO=O,∴CO⊥平面AOB,
又CO?平面COD,∴平面COD⊥平面AOB.
解:(Ⅱ)當VA-DOC:VA-BOC=1:2時,D為AB中點,
以O為原點,OC為x軸,OB為y軸,OA為z軸,建立空間直角坐標系O-xyz,如圖,
則B(0,2,0),A(0,0,2$\sqrt{3}$),C(2,0,0),D(0,1,$\sqrt{3}$),
∴$\overrightarrow{CD}$=(-2,1,$\sqrt{3}$),
平面AOB的法向量$\overrightarrow{n}$=(1,0,0),
設CD與平面AOB所成角為θ,
則sinθ=$\frac{|\overrightarrow{CD}•\overrightarrow{n}|}{|\overrightarrow{CD}|•|\overrightarrow{n}|}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
∴θ=45°.
∴CD與平面AOB所成角為45°.
點評 本題考查面面垂直的證明,考查線面角的求法,是中檔題,解題時要認真審題,注意向量法的合理運用.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
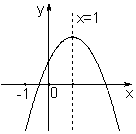 二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列4個結論①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;
二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列4個結論①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{\sqrt{15}}{15}$ | B. | $\frac{\sqrt{15}}{15}$ | C. | $\frac{2\sqrt{15}}{15}$ | D. | $\frac{\sqrt{15}}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com