
【題目】微信是現代生活進行信息交流的重要工具,隨機對使用微信的60人進行了統計,得到如下數據統計表,每天使用微信時間在兩小時以上的人被定義為“微信達人”,不超過2兩小時的人被定義為“非微信達人”,己知“非微信達人”與“微信達人”人數比恰為3:2. 
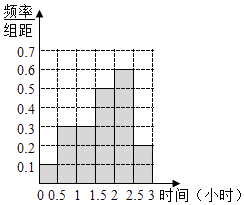
(1)確定x,y,p,q的值,并補全須率分布直方圖;
(2)為進一步了解使用微信對自己的日不工作和生活是否有影響,從“微信達人”和“非微信達人”60人中用分層抽樣的方法確定10人,若需從這10人中隨積選取3人進行問卷調查,設選取的3人中“微信達人”的人數為X,求X的分布列和數學期望.
使用微信時間(單位:小時) | 頻數 | 頻率 |
(0,0.5] | 3 | 0.05 |
(0.5,1] | x | p |
(1,1.5] | 9 | 0.15 |
(1.5,2] | 15 | 0.25 |
(2,2.5] | 18 | 0.30 |
(2.5,3] | y | q |
合計 | 60 | 1.00 |
【答案】
(1)解:根據題意,有
 ,
,
解得x=9,y=6,
∴p=0.15,q=0.10,
補全頻率分布圖有右圖所示
(2)解:用分層抽樣的方法,從中選取10人,則其中“網購達人”有10× ![]() =4人,“非網購達人”有10×
=4人,“非網購達人”有10× ![]() =6人,
=6人,
∴ξ的可能取值為0,1,2,3,
P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列為:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =
= ![]() .
.
【解析】(1)根據分布直方圖、頻率分布表的性質,列出方程組,能確定x,y,p,q的值,并補全須率分布直方圖.(2)用分層抽樣的方法,從中選取10人,則其中“網購達人”有4人,“非網購達人”有6人,ξ的可能取值為0,1,2,3,分別求出相應的概率,由此能求出ξ的分布列和數學期望.
【考點精析】本題主要考查了頻率分布直方圖和離散型隨機變量及其分布列的相關知識點,需要掌握頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息;在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列才能正確解答此題.


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:
【題目】已知焦距為2 ![]() 的橢圓C:
的橢圓C: ![]() +
+ ![]() =1(a>b>0)的右頂點為A,直線y=
=1(a>b>0)的右頂點為A,直線y= ![]() 與橢圓C交于P、Q兩點(P在Q的左邊),Q在x軸上的射影為B,且四邊形ABPQ是平行四邊形.
與橢圓C交于P、Q兩點(P在Q的左邊),Q在x軸上的射影為B,且四邊形ABPQ是平行四邊形.
(1)求橢圓C的方程;
(2)斜率為k的直線l與橢圓C交于兩個不同的點M,N.
(i)若直線l過原點且與坐標軸不重合,E是直線3x+3y﹣2=0上一點,且△EMN是以E為直角頂點的等腰直角三角形,求k的值
(ii)若M是橢圓的左頂點,D是直線MN上一點,且DA⊥AM,點G是x軸上異于點M的點,且以DN為直徑的圓恒過直線AN和DG的交點,求證:點G是定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() sinxcosx﹣3sin2x﹣cos2x+3.
sinxcosx﹣3sin2x﹣cos2x+3.
(1)當x∈[0, ![]() ]時,求f(x)的值域;
]時,求f(x)的值域;
(2)若△ABC的內角A,B,C的對邊分別為a,b,c,且滿足 ![]() =
= ![]() ,
, ![]() =2+2cos(A+C),求f(B)的值.
=2+2cos(A+C),求f(B)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O1和圓O2的極坐標方程分別為ρ=2, ![]() .
.
(1)把圓O1和圓O2的極坐標方程化為直角坐標方程;
(2)求經過兩圓交點的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F1、F2是雙曲線 ![]() =1(a>0,b>0)的左、右焦點,P是雙曲線右支上一點,滿足(
=1(a>0,b>0)的左、右焦點,P是雙曲線右支上一點,滿足( ![]() +
+ ![]() )
) ![]() =0(O為坐標原點),且3|
=0(O為坐標原點),且3| ![]() |=4|
|=4| ![]() |,則雙曲線的離心率為( )
|,則雙曲線的離心率為( )
A.2
B.![]()
C.![]()
D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=|x﹣a|,a∈R
(Ⅰ)當a=5,解不等式f(x)≤3;
(Ⅱ)當a=1時,若x∈R,使得不等式f(x﹣1)+f(2x)≤1﹣2m成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用如圖所示的幾何體中,四邊形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1 , E是AC的中點. 
(1)求證:A1E∥平面BB1C1C;
(2)若AC=BC,AB=2BB1 , 求二面角A﹣BA1﹣E的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中,正確的有( )
①不存在實數k,使得方程xlnx﹣ ![]() x2+k=0有兩個不等實根;
x2+k=0有兩個不等實根;
②已知△ABC中,a,b,c分別為角A,B,C的對邊,且a2+b2=2c2 , 則角C的最大值為 ![]() ;
;
③函數y= ![]() ln
ln ![]() 與y=lntan
與y=lntan ![]() 是同一函數;
是同一函數;
④在橢圓 ![]() +
+ ![]() =1(a>b>0),左右頂點分別為A,B,若P為橢圓上任意一點(不同于A,B),則直線PA與直線PB斜率之積為定值.
=1(a>b>0),左右頂點分別為A,B,若P為橢圓上任意一點(不同于A,B),則直線PA與直線PB斜率之積為定值.
A.①④
B.①③
C.①②
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面ACC1A1與側面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2 ![]() .
. 
(1)求證:AB1⊥CC1;
(2)若AB1=3 ![]() ,A1C1的中點為D1 , 求二面角C﹣AB1﹣D1的余弦值.
,A1C1的中點為D1 , 求二面角C﹣AB1﹣D1的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com