
【題目】已知二次函數f(x)的二次項系數為a(a<0).1,3是函數y=f(x)+2x的兩個零點.若方程f(x)+6a=0有兩個相等的根,求f(x)的解析式.
【答案】f(x)=-![]() x2-
x2-![]() x-
x-![]() .
.
【解析】
由題意,利用待定系數法,f(x)+2x=a(x-1)(x-3),則f(x)+6a=ax2-(2+4a)x+9a=0.利用方程的判別式可得a=-![]() .則f(x)=-
.則f(x)=-![]() x2-
x2-![]() x-
x-![]() .
.
因為1,3是y=f(x)+2x的兩個零點,且a<0,
所以f(x)+2x=a(x-1)(x-3),
得f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a.①
所以f(x)+6a=ax2-(2+4a)x+9a=0.②
又方程②有兩個相等的實根,
所以Δ=[-(2+4a)]2-4a·9a=0,
即5a2-4a-1=0,
解得a=1(舍去)或a=-![]() .
.
將a=-![]() 代入①,得
代入①,得
f(x)=-![]() x2-
x2-![]() x-
x-![]() .
.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】某輪船公司的一艘輪船每小時花費的燃料費與輪船航行速度的平方成正比,比例系數為![]() 輪船的最大速度為15海里
輪船的最大速度為15海里![]() 小時
小時![]() 當船速為10海里
當船速為10海里![]() 小時,它的燃料費是每小時96元,其余航行運作費用(不論速度如何)總計是每小時150元
小時,它的燃料費是每小時96元,其余航行運作費用(不論速度如何)總計是每小時150元![]() 假定運行過程中輪船以速度v勻速航行.
假定運行過程中輪船以速度v勻速航行.
![]() 求k的值;
求k的值;
![]() 求該輪船航行100海里的總費用
求該輪船航行100海里的總費用![]() 燃料費
燃料費![]() 航行運作費用
航行運作費用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C: ![]() +
+ ![]() =1,直線l:
=1,直線l: ![]() (t為參數)
(t為參數)
(1)寫出曲線C的參數方程,直線l的普通方程.
(2)過曲線C上任意一點P作與l夾角為30°的直線,交l于點A,求|PA|的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某學校準備修建一個面積為2400平方米的矩形活動場地(圖中ABCD)的圍欄,按照修建要求,中間用圍墻EF隔開,使得ABEF為矩形,EFCD為正方形,設![]() 米,已知圍墻(包括EF)的修建費用均為每米500元,設圍墻(包括EF)的修建總費用為y元.
米,已知圍墻(包括EF)的修建費用均為每米500元,設圍墻(包括EF)的修建總費用為y元.
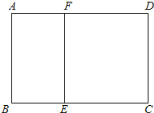
(1)求出y關于x的函數解析式及x的取值范圍;
(2)當x為何值時,圍墻(包括EF)的修建總費用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=3x,f(a+2)=27,函數g(x)=λ·2ax-4x的定義域為[0,2].
(1)求a的值;
(2)若函數g(x)在[0,2]上單調遞減,求λ的取值范圍;
(3)若函數g(x)的最大值是![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 經過
經過![]() ,
,![]() ,
,![]() ,
,![]() 三點,
三點,![]() 是線段
是線段![]() 上的動點,
上的動點,![]() ,
,![]() 是過點
是過點![]() 且互相垂直的兩條直線,其中
且互相垂直的兩條直線,其中![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 交圓
交圓![]() 于
于![]() 、
、![]() 兩點.
兩點.
(1)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)若![]() 是使
是使![]() 恒成立的最小正整數,求三角形
恒成立的最小正整數,求三角形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個不相等的非零向量 ![]() ,
, ![]() ,兩組向量
,兩組向量 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均由2個
均由2個 ![]() 和3個
和3個 ![]() 排列而成,記S=
排列而成,記S= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ,Smin表示S所有可能取值中的最小值.則下列命題正確的是(寫出所有正確命題的編號).
,Smin表示S所有可能取值中的最小值.則下列命題正確的是(寫出所有正確命題的編號).
①S有5個不同的值;
②若 ![]() ⊥
⊥ ![]() ,則Smin與|
,則Smin與| |無關;
③若 ![]() ∥
∥ ![]() ,則Smin與|
,則Smin與| ![]() |無關;
|無關;
④若| ![]() |>4|
|>4| ![]() |,則Smin>0;
|,則Smin>0;
⑤若| ![]() |=2|
|=2| ![]() |,Smin=8|
|,Smin=8| ![]() |2 , 則
|2 , 則 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com