【題目】已知函數(shù)f（x）=x2﹣cosx，x∈[﹣ 
， ]，則滿足f（x0）＞f（ 
）的x0的取值范圍為 ．
【答案】[﹣ 
,﹣ 
）∪（ , ]
【解析】解：注意到函數(shù)f（x）=x2﹣cosx，x∈[﹣ 
， ]是偶函數(shù)，
故只需考慮[0， ]區(qū)間上的情形．
當x∈[0， ]時，f′（x）=2x+sinx≥0，
∴函數(shù)在[0， ]單調(diào)遞增，
所以f（x0）＞f（ 
）在[0， ]上的解集為（ ， ]，
結合函數(shù)是偶函數(shù)，圖象關于y軸對稱，
得原問題中x0取值范圍是[﹣ ，﹣ ）∪（ ， ]，
所以答案是：[﹣ ，﹣ ）∪（ ， ]．
【考點精析】解答此題的關鍵在于理解利用導數(shù)研究函數(shù)的單調(diào)性的相關知識，掌握一般的,函數(shù)的單調(diào)性與其導數(shù)的正負有如下關系： 在某個區(qū)間
內(nèi)，(1)如果
，那么函數(shù)
在這個區(qū)間單調(diào)遞增；(2)如果
，那么函數(shù)
在這個區(qū)間單調(diào)遞減．
科目：高中數(shù)學 來源： 題型：
【題目】已知
是定義在
上的奇函數(shù)，且
，若
，
時，有
成立.
（Ⅰ）判斷在上的單調(diào)性，并證明；
（Ⅱ）解不等式
；
（Ⅲ）若
對所有的
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知向量
，記
．
（Ⅰ）求
的單調(diào)遞減區(qū)間；
（Ⅱ）若
，求 
的值；
（Ⅲ）將函數(shù)
的圖象向右平移
個單位得到
的圖象，若函數(shù)
在
上有零點，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=|x+a|．
（1）若a=2，解關于x的不等式f（x）+f（x﹣3）≥5；
（2）若關于x的不等式f（x）﹣f（x+2）+4≥|1﹣3m|恒成立，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）=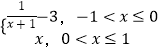 
，若函數(shù)g（x）=f（x）﹣mx﹣m在（﹣1，1]內(nèi)有且僅有兩個不同的零點，則實數(shù)m的取值范圍為 ．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖所示，四棱錐 
的底面為直角梯形， 
， 
， 
， 
， 
底面 
， 
為 
的中點.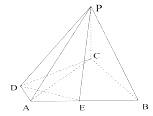
（Ⅰ）求證：平面 
平面 
（Ⅱ）求直線 
與平面 
所成的角的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
是定義在
上的奇函數(shù)，且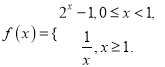
偶函數(shù)
的定義域為
，且當
時， 
.若存在實數(shù)
，使得
成立，則實數(shù)
的取值范圍是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
