
【題目】如圖,矩形![]() 所在的平面與直角梯形
所在的平面與直角梯形![]() 所在的平面成
所在的平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
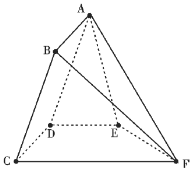
(1)求證:![]() 面
面![]() ;
;
(2)在線段![]() 上求一點
上求一點![]() ,使銳二面角
,使銳二面角![]() 的余弦值為
的余弦值為![]() .
.
【答案】(1)見解析;(2)![]() 為線段
為線段![]() 的中點.
的中點.
【解析】
(1)利用面面平行的判定定理證明出平面![]() 平面
平面![]() ,再利用平面與平面平行的性質得出
,再利用平面與平面平行的性質得出![]() 平面
平面![]() ;
;
(2)由![]() ,
,![]() ,由二面角的定義得出
,由二面角的定義得出![]() ,證明出平面
,證明出平面![]() 平面
平面![]() ,過點
,過點![]() 在平面
在平面![]() 內作
內作![]() ,可證明出
,可證明出![]() 平面
平面![]() ,以點
,以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,設點
,設點![]() 的坐標為
的坐標為![]() ,利用向量法結合條件銳二面角的余弦值為
,利用向量法結合條件銳二面角的余弦值為![]() 求出
求出![]() 的值,由此確定點
的值,由此確定點![]() 的位置.
的位置.
(1)在矩形![]() 中,
中,![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,同理可證
,同理可證![]() 平面
平面![]() ,
,
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)在矩形![]() 中,
中,![]() ,又
,又![]() ,則矩形
,則矩形![]() 所在平面與直角梯形所在平面所成二面角的平面角為
所在平面與直角梯形所在平面所成二面角的平面角為![]() ,即
,即![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
作![]() 于
于![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
作![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
以![]() 為原點,
為原點,![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸如圖建立空間直角坐標系
軸如圖建立空間直角坐標系![]() ,
,
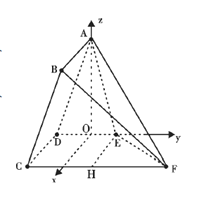
則![]() 、
、![]() ,設
,設![]() .
.
則![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則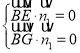 ,即
,即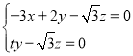 ,取
,取![]() ,則
,則![]() ,
,![]() ,則平面
,則平面![]() 的一個法向量為
的一個法向量為![]() .
.
.又平面![]() 的一個法向量為
的一個法向量為![]() ,
,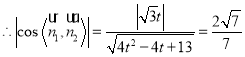 ,
,
解得![]() 或
或![]() (舍去).
(舍去).
此時,![]() ,
,![]() 即所求點
即所求點![]() 為線段
為線段![]() 的中點.
的中點.


科目:高中數學 來源: 題型:
【題目】有甲、乙二人去看望高中數學張老師,期間他們做了一個游戲,張老師的生日是![]() 月
月![]() 日,張老師把
日,張老師把![]() 告訴了甲,把
告訴了甲,把![]() 告訴了乙,然后張老師列出來如下10個日期供選擇: 2月5日,2月7日,2月9日,3月2日,3月7日,5月5日,5月8日,7月2日,7月6日,7月9日.看完日期后,甲說“我不知道,但你一定也不知道”,乙聽了甲的話后,說“本來我不知道,但現在我知道了”,甲接著說,“哦,現在我也知道了”.請問張老師的生日是_______.
告訴了乙,然后張老師列出來如下10個日期供選擇: 2月5日,2月7日,2月9日,3月2日,3月7日,5月5日,5月8日,7月2日,7月6日,7月9日.看完日期后,甲說“我不知道,但你一定也不知道”,乙聽了甲的話后,說“本來我不知道,但現在我知道了”,甲接著說,“哦,現在我也知道了”.請問張老師的生日是_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某養殖產品在某段時間內的生長情況,在該批產品中隨機抽取了120件樣本,測量其增長長度(單位:![]() ),經統計其增長長度均在區間
),經統計其增長長度均在區間![]() 內,將其按
內,將其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,制成頻率分布直方圖,如圖所示其中增長長度為
分成6組,制成頻率分布直方圖,如圖所示其中增長長度為![]() 及以上的產品為優質產品.
及以上的產品為優質產品.

(1)求圖中![]() 的值;
的值;
(2)已知這120件產品來自于![]() ,B兩個試驗區,部分數據如下列聯表:
,B兩個試驗區,部分數據如下列聯表:

將聯表補充完整,并判斷是否有99.99%的把握認為優質產品與A,B兩個試驗區有關系,并說明理由;
下面的臨界值表僅供參考:

(參考公式: ,其中
,其中![]() )
)
(3)以樣本的頻率代表產品的概率,從這批產品中隨機抽取4件進行分析研究,計算抽取的這4件產品中含優質產品的件數![]() 的分布列和數學期望E(X).
的分布列和數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現對某市工薪階層關于“樓市限購令”的態度進行調查,隨機抽調了![]() 人,他們月收入的頻數分布及對“樓市限購令”贊成人數如下表.
人,他們月收入的頻數分布及對“樓市限購令”贊成人數如下表.
月收入(單位百元) |
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
贊成人數 |
|
|
|
|
|
|
(1)由以上統計數據填下面![]() 列聯表,并問是否有
列聯表,并問是否有![]() 的把握認為“月收入以
的把握認為“月收入以![]() 元為分界點對“樓市限購令”的態度有差異;
元為分界點對“樓市限購令”的態度有差異;
月收入不低于 | 月收入低于 | 合計 | |
贊成 |
|
| ______________ |
不贊成 |
|
| ______________ |
合計 | ______________ | ______________ | ______________ |
(2)若對在![]() 、
、![]() 的被調查者中各隨機選取兩人進行追蹤調查,記選中的
的被調查者中各隨機選取兩人進行追蹤調查,記選中的![]() 人中不贊成“樓市限購令”的人數為
人中不贊成“樓市限購令”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式: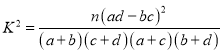 ,其中
,其中![]() .
.
參考值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到焦點
到焦點![]() 的距離
的距離![]() ,傾斜角為
,傾斜角為![]() 的直線經過焦點
的直線經過焦點![]() ,且與拋物線交于兩點
,且與拋物線交于兩點![]() 、
、![]() .
.
(1)求拋物線的標準方程及準線方程;
(2)若![]() 為銳角,作線段
為銳角,作線段![]() 的中垂線
的中垂線![]() 交
交![]() 軸于點
軸于點![]() .證明:
.證明:![]() 為定值,并求出該定值.
為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 在
在![]() 上的單調遞增區間;
上的單調遞增區間;
(2)將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再將圖象上所有點的橫坐標伸長到原來的
個單位長度,再將圖象上所有點的橫坐標伸長到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象.求證:存在無窮多個互不相同的整數
的圖象.求證:存在無窮多個互不相同的整數![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某種產品的年固定成本為250萬元,每生產![]() 千件,需另投入成本
千件,需另投入成本![]() ,當年產量不足80千件時,
,當年產量不足80千件時,![]() (萬元);當年產量不小于80千件時,
(萬元);當年產量不小于80千件時,![]() (萬元),每件售價為0.05萬元,通過市場分析,該廠生產的商品能全部售完.
(萬元),每件售價為0.05萬元,通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com