
【題目】已知關于x的不等式ax2+bx+c>0的解集為{x|2<x<3},求關于x的不等式cx2+bx+a<0的解集.
【答案】![]() 或
或![]() .
.
【解析】
根據一元二次不等式的解,得出對應一元二次方程的解,進而得到![]() 關系,化簡不等式,即可求解.
關系,化簡不等式,即可求解.
法一:由不等式ax2+bx+c>0的解集為{x|2<x<3}可知,a<0,
且2和3是方程ax2+bx+c=0的兩根,
由根與系數的關系可知![]() .
.
由a<0,故不等式cx2+bx+a<0化為,![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() ,
,
所以不等式cx2+bx+a<0的解集為![]() 或
或![]() .
.
法二:由不等式ax2+bx+c>0的解集為{x|2<x<3}可知,
a<0,且2和3是方程ax2+bx+c=0的兩根,
所以ax2+bx+c=a(x-2)(x-3)=ax2-5ax+6ab=-5a,c=6a,
故不等式cx2+bx+a<0,即6ax2-5ax+a<06a![]() ,
,
故原不等式的解集為![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】某次數學知識比賽中共有6個不同的題目,每位同學從中隨機抽取3個題目進行作答,已知這6個題目中,甲只能正確作答其中的4個,而乙正確作答每個題目的概率均為![]() ,且甲、乙兩位同學對每個題目的作答都是相互獨立、互不影響的.
,且甲、乙兩位同學對每個題目的作答都是相互獨立、互不影響的.
(1)求乙同學答對2個題目的概率;
(2)若甲、乙兩位同學答對題目個數分別是m,n,分別求出甲、乙兩位同學答對題目個數m,n的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() ,將函數
,將函數![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖像.
的圖像.
(1)求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)在銳角![]() 中,角
中,角![]() 的對邊分別為
的對邊分別為![]() ,若
,若![]() ,
,![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知sin(-π+θ)+2cos(3π-θ)=0,則![]() ;
;
(2)已知![]() .
.
①化簡f(α);
②若f(α)![]() ,且
,且![]() ,求cos α-sin α的值;
,求cos α-sin α的值;
③若![]()
![]() ,求f(α)的值.
,求f(α)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() ,數列
,數列![]() 滿足條件:對于
滿足條件:對于![]() ,
,![]() ,且
,且![]() ,并有關系式:
,并有關系式:![]() ,又設數列
,又設數列![]() 滿足
滿足![]() (
(![]() 且
且![]() ,
,![]() ).
).
(1)求證數列![]() 為等比數列,并求數列
為等比數列,并求數列![]() 的通項公式;
的通項公式;
(2)試問數列![]() 是否為等差數列,如果是,請寫出公差,如果不是,說明理由;
是否為等差數列,如果是,請寫出公差,如果不是,說明理由;
(3)若![]() ,記
,記![]() ,
,![]() ,設數列
,設數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,若對任意的
,若對任意的![]() ,不等式
,不等式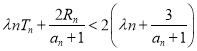 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程是 (φ為參數,a>0),直線l的參數方程是
(φ為參數,a>0),直線l的參數方程是![]() (t為參數),曲線C與直線l有一個公共點在x軸上,以坐標原點為極點,x軸的正半軸為極軸建立坐標系.
(t為參數),曲線C與直線l有一個公共點在x軸上,以坐標原點為極點,x軸的正半軸為極軸建立坐標系.
(1)求曲線C的普通方程;
(2)若點A(ρ1,θ),B(ρ2,θ+![]() ),C(ρ3,θ+
),C(ρ3,θ+![]() )在曲線C上,求
)在曲線C上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com