
某商場經營一批進價是30元/件的商品,在市場試銷中發現,此商品銷售價 元與日銷售量
元與日銷售量 件之間有如下關系:
件之間有如下關系:
x | 45 | 50 |
y | 27 | 12 |
(I)確定 與
與 的一個一次函數關系式
的一個一次函數關系式 ;
;
(Ⅱ)若日銷售利潤為P元,根據(I)中關系寫出P關于 的函數關系,并指出當銷售單價為多少元時,才能獲得最大的日銷售利潤?
的函數關系,并指出當銷售單價為多少元時,才能獲得最大的日銷售利潤?
(I)y=162-3x(0≤x≤54);(Ⅱ)銷售單價為42元/件時,獲得最大日銷售利潤;
【解析】
試題分析:(1)由題意可知 為一次函數,有待定系數法求出解析式;
為一次函數,有待定系數法求出解析式;
(2)銷售利潤函數=(售價-進價)×銷量,代入數值得二次函數,求出最值.
試題解析:(1)因為f(x)為一次函數,設y=ax+b,解方程組
 2分
2分
得a=-3,b=162, 4分
故y=162-3x為所求的函數關系式,
又∵y≥0,∴0≤x≤54. 6分
(2)依題意得:
P=(x-30)·y=(x-30)·(162-3x) 8分
=-3(x-42)2+432. 10分
當x=42時,P最大=432,
即銷售單價為42元/件時,獲得最大日銷售利潤. 12分
考點:函數模型的選擇與應用.


科目:高中數學 來源:2016屆浙江省杭州市外國語學校高一期中考試數學試卷(解析版) 題型:解答題
已知定義在 上的函數
上的函數 ,如果滿足:對任意
,如果滿足:對任意 ,存在常數
,存在常數 ,使得
,使得 成立,則稱
成立,則稱 是
是 上的有界函數,其中
上的有界函數,其中 稱為函數
稱為函數 的上界.
的上界.
下面我們來考慮兩個函數: ,
, .
.
(Ⅰ)當 時,求函數
時,求函數 在
在 上的值域,并判斷函數
上的值域,并判斷函數 在
在 上是否為有界函數,請說明理由;
上是否為有界函數,請說明理由;
(Ⅱ)若 ,函數
,函數 在
在 上的上界是
上的上界是 ,求
,求 的取值范圍;
的取值范圍;
(Ⅲ)若函數 在
在 上是以
上是以 為上界的有界函數, 求實數
為上界的有界函數, 求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2016屆河南省鄭州市高一上學期期末考試數學試卷(解析版) 題型:選擇題
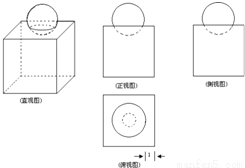
如圖是一個簡單的組合體的直觀圖與三視圖,一個棱長為4的正方體,正上面中心放一個球,且球的一部分嵌入正方體中,則球的半徑是( )
A. 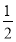 B. 1 C.
B. 1 C. 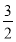 D. 2
D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com