
【題目】已知函數![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)當![]() 時,求
時,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在實數![]() 、
、![]() ,同時滿足下列條件:①
,同時滿足下列條件:① ![]() ;② 當
;② 當![]() 的定義域為
的定義域為![]() 時,其值域為
時,其值域為![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1) ![]() (2)
(2)  (3) 不存在滿足條件的實數
(3) 不存在滿足條件的實數![]() 、
、![]() .見解析
.見解析
【解析】
(1)設t=3x,則φ(t)=t2﹣2at+3=(t﹣a)2+3﹣a2,φ(t)的對稱軸為t=a,當a=1時,即可求出f(x)的值域;
(2)由函數φ(t)的對稱軸為t=a,分類討論當a![]() 時,當
時,當![]() a≤3時,當a>3時,求出最小值,則h(a)的表達式可求;
a≤3時,當a>3時,求出最小值,則h(a)的表達式可求;
(3)假設滿足題意的m,n存在,函數h(a)在(3,+∞)上是減函數,求出h(a)的定義域,值域,然后列出不等式組,求解與已知矛盾,即可得到結論.
(1)當![]() 時,由
時,由![]() ,得
,得![]() ,
,
因為![]() ,所以
,所以![]() ,
,![]() .
.
(2)令![]() ,因為
,因為![]() ,故
,故![]() ,函數
,函數![]() 可化為
可化為
![]() .
.
① 當![]() 時,
時,![]() ;
;
② 當![]() 時,
時,![]() ;
;
③ 當![]() 時,
時,![]() .
.
綜上,
(3)因為![]() ,
,![]() 為減函數,
為減函數,
所以![]() 在
在![]() 上的值域為
上的值域為![]() ,
,
又![]() 在
在![]() 上的值域為
上的值域為![]() ,所以,
,所以,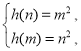 即
即
兩式相減,得![]() ,
,
因為![]() ,所以
,所以![]() ,而由
,而由![]() 可得
可得![]() ,矛盾.
,矛盾.
所以,不存在滿足條件的實數![]() 、
、![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,若對于
,若對于![]() 分別為某個三角形的邊長,則稱
分別為某個三角形的邊長,則稱![]() 為“三角形函數”.給出下列四個函數:
為“三角形函數”.給出下列四個函數:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中為“三角形函數”的個數是( )
.其中為“三角形函數”的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產的某種產品被檢測出其中一項質量指標存在問題.該企業為了檢查生產該產品的甲、乙兩條流水線的生產情況,隨機地從這兩條流水線上生產的大量產品中各抽取50件產品作為樣本,測出它們的這一項質量指標值.若該項質量指標值落在![]() 內,則為合格品,否則為不合格品.如圖是甲流水線樣本的頻數分布表和乙流水線樣本的頻率分布直方圖.
內,則為合格品,否則為不合格品.如圖是甲流水線樣本的頻數分布表和乙流水線樣本的頻率分布直方圖.
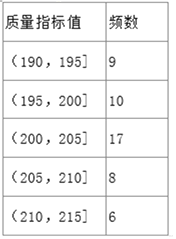
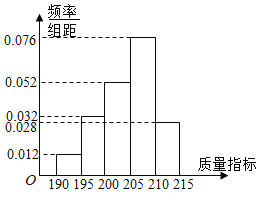
(1)根據頻率分布直方圖,估計乙流水線生產的產品該質量指標值的中位數;
(2)若將頻率視為概率,某個月內甲、乙兩條流水線均生產了5000件產品,則甲、乙兩條流水線分別生產出不合格品約多少件?
(3)根據已知條件完成下面![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為“該企業生產的這種產品的質量指標值與甲、乙兩條流水線的選擇有關”?
的把握認為“該企業生產的這種產品的質量指標值與甲、乙兩條流水線的選擇有關”?
甲流水線 | 乙流水線 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
附:![]() ,其中
,其中![]() .
.
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中,![]() 分別是
分別是![]() 的中點將
的中點將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 重合于點
重合于點![]() .則下列結論正確的是( )
.則下列結論正確的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值為
的余弦值為![]()
D. 點![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市甲、乙兩地為了爭創“市級文明城市”,現市文明委對甲、乙兩地各派10名專家進行打分評優,所得分數情況如下莖葉圖所示.
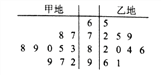
(1)分別計算甲、乙兩地所得分數的平均值,并計算乙地得分的中位數;
(2)從乙地所得分數在![]() 間的成績中隨機抽取2份做進一步分析,求所抽取的成績中,至少有一份分數在
間的成績中隨機抽取2份做進一步分析,求所抽取的成績中,至少有一份分數在![]() 間的概率;
間的概率;
(3)在甲、乙兩地所得分數超過90分的成績中抽取其中2份分析其合理性,求這2份成績都是來自甲地的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國著名數學家狄利克雷在數學領域成就顯著,以其名命名的函數 被稱為狄利克雷函數,其中
被稱為狄利克雷函數,其中![]() 為實數集,
為實數集,![]() 為有理數集,則關于函數
為有理數集,則關于函數![]() 有如下四個命題:①
有如下四個命題:①![]() ;②函數
;②函數![]() 是偶函數;③任取一個不為零的有理數
是偶函數;③任取一個不為零的有理數![]() ,
,![]() 對任意的
對任意的![]() 恒成立;④存在三個點
恒成立;④存在三個點![]() ,
,![]() ,
,![]() ,使得
,使得![]() 為等邊三角形.其中真命題的個數有( )
為等邊三角形.其中真命題的個數有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.

(1)用分段函數的形式表示函數![]() 的解析式,并畫出
的解析式,并畫出![]() 在
在![]() 上的大致圖像;
上的大致圖像;
(2)若關于x的方程![]() 恰有一個實數解,求出實數m的取值范圍組成的集合;
恰有一個實數解,求出實數m的取值范圍組成的集合;
(3)當![]() 時,求函數
時,求函數![]() 的值域.
的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com