
| 1 |
| 2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2na1a2an | ||
|
| 2na1a2an | ||
|
| 2n+1×1×2××n×(n+1) | ||
|
| g(n+1) |
| g(n) |
| 2n+2 | ||||
|
|
2
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2na1a2an | ||
|
| 2na1a2an | ||
|
| 2n+1×1×2××n×(n+1) | ||
|
| g(n+1) |
| g(n) |
| 2n+2 | ||||
|
|
2
| ||
| 3 |
2
| ||
| 3 |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2009-2010學年廣東省廣州市育才中學高三(上)摸底數學試卷(文科)(解析版) 題型:解答題
 .
.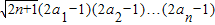 對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.
對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:2011年廣東省高考數學全真模擬試卷6(理科)(解析版) 題型:解答題
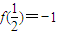 .
.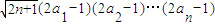 對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.
對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:2008-2009學年廣東省惠州市高三第二次調研數學試卷(理科)(解析版) 題型:解答題
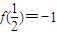 .
.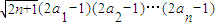 對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.
對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:2010年湖北省黃岡市名校高考數學模擬試卷08(理科)(解析版) 題型:解答題
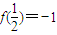 .
.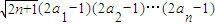 對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.
對一切n∈N*成立?若存在,求出M的取值范圍;若不存在,請說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com