Question

甲、乙兩地相距s千米，汽車從甲地勻速駛到乙地，速度不得超過c千米/時，已知汽車每小時的運輸成本（以元為單位）由可變部分和固定部分組成：可變部分與速度v(千米/時)的平方成正比，比例系數為b；固定部分為a元.

（1）把全程運輸成本y（元）表示為速度v(千米/時)的函數，并指出這個函數的定義域；

（2）為了使全程運輸成本最小，汽車應以多大速度行駛？

Answer 1

思路解析：本題寫出函數y=f(v)=(+bv)s及其定義域（0,c）并不難，在運用不等式的平均值定理求y的最小值時，確定其中等號成立條件時,要由=bv解出v=后檢驗是否在函數定義域（0,c］內.這時要對與c的大小作出討論,并且對于＞c的情形，求y的最小值還要另選方法，即選擇通過研究函數單調性而確定其最值的方法.這是一種運用概念的一般方法，不過運用時過程比較煩瑣就是了.

解：（1）依題意得汽車從甲地勻速行駛到乙地所用時間為（時），全程運輸成本為y=a·+bv²·=s(+bv).

∴函數為y=s(+bv)，其定義域為（0,c）.

（2）依題意得s、a、b、v均為正數，則s(+bv)≥2s=2s.當且僅當=bv，即v=時，上式“≥”處等號成立.

若≤c，則當v=時，y取最小值.

若＞c時，任取v₁、v₂，使0＜v₁＜v₂≤c＜,

則(+bv₂)-(+bv₁)=b(v₂-v₁)+a()=(bv₁v₂-a).

由于v₁v₂＞0,v₂-v₁＞0，并且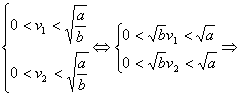bv₁v₂＜a，

∴+bv₂＜+bv₁.

又s＞0,故s(+bv₂)＜s(+bv₁).

∴當＞c時，v的函數y=s(+bv)在區間（0,c］上是減函數，當v=c時，y取最小值.

綜上，可知為了使全程運輸成本最小，當≤c時，汽車行駛速度應為v=（千米/時）；當＞c時，汽車行駛速度應為v=c（千米/時）.