Question

【例】

已知函數y=sin2x+cos2x－2.

（1）用“五點法”作出函數在一個周期內的圖象;

（2）求這個函數的周期和單調區間;

（3）求函數圖象的對稱軸方程.

（4）說明圖象是由y=sinx的圖象經過怎樣的變換得到的.

學科網

Answer 1

T==π，單調增區間為［－π+kπ+kπ］，k∈Z;，函數的單調減區間為［+kπ，π+kπ］，k∈Z

解析:

解: y=sin2x+cos2x－2=2sin（2x+）－2.

（1）列表

x	－			π	π
2x+	0		π	π	2π
y=2sin（2x+）－2	－2	0	－2	－4	－2

 其圖象如下圖所示.

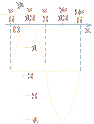
（2）T==π.

由－+2kπ≤2x+≤+2kπ，知函數的單調增區間為［－π+kπ+kπ］，k∈Z;

由+2kπ≤2x+≤π+2kπ，知函數的單調減區間為［+kπ，π+kπ］，k∈Z.

（3）由2x+=+kπ得x=+π.

∴函數圖象的對稱軸方程為x=+π（k∈Z）.

（4）把函數y₁=sinx的圖象上所有的點向左平移個單位，得到函數y₂=sin（x+）的圖象；

再把y₂圖象上各點的橫坐標縮短到原來的倍（縱坐標不變），得到y₃=sin（2x+）的圖象；

再把y₃圖象上各點的縱坐標伸長到原來的2倍（橫坐標不變），得到y₄=2sin（2x+）的圖象；

最后把y₄圖象上所有的點向下平移2個單位，得到函數y=2sin（2x+）－2的圖象.

評注:（1）求函數的周期、單調區間、最值等問題，一般都要化成一個角的三角函數形式.

（2）對于函數y=Asin（ωx+）的對稱軸，實際上就是使函數y取得最大值或最小值時的x值.

（3）第（4）問的變換方法不唯一，但必須特別注意平移變換與伸縮變換的先后順序.