
【題目】已知函數![]() ,其中函數
,其中函數![]() 的圖象在點
的圖象在點![]() 處的切線平行于
處的切線平行于![]() 軸.
軸.
(1)確定![]() 與
與![]() 的關系;
的關系;
(2)若![]() ,試討論函數
,試討論函數![]() 的單調性.
的單調性.
【答案】(1)![]() ,(2)當
,(2)當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
【解析】
試題分析:(1)依題意得![]() ,
,
則![]() .
.
由函數![]() 的圖象在點
的圖象在點![]() 處的切線平行于
處的切線平行于![]() 軸得:
軸得:![]() ,∴
,∴![]() .
.
(2)由(1)得![]() .
.
∵函數![]() 的定義域為
的定義域為![]() ,
,
∴當![]() 時,
時,![]() .
.
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
當![]() 時,令
時,令![]() ,得
,得![]() 或
或![]() ,
,
若![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
由![]() ,得
,得![]() ;
;
若![]() ,即
,即![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
由![]() ,得
,得![]() .
.
若![]() ,即
,即![]() ,在
,在![]() 上恒有
上恒有![]() .
.
綜上可得:當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】現有甲、乙兩個項目,對甲項目每投資10萬元,一年后利潤是1.2萬元、1.18萬元、1.17萬元的概率分別為![]() ;已知乙項目的利潤與產品價格的調整有關,在每次調整中,價格下降的概率都是p(0<p<1),設乙項目產品價格在一年內進行兩次獨立的調整.記乙項目產品價格在一年內的下降次數為X,對乙項目每投資10萬元,X取0、1、2時,一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量X1、X2分別表示對甲、乙兩項目各投資10萬元一年后的利潤.
;已知乙項目的利潤與產品價格的調整有關,在每次調整中,價格下降的概率都是p(0<p<1),設乙項目產品價格在一年內進行兩次獨立的調整.記乙項目產品價格在一年內的下降次數為X,對乙項目每投資10萬元,X取0、1、2時,一年后相應利潤是1.3萬元、1.25萬元、0.2萬元.隨機變量X1、X2分別表示對甲、乙兩項目各投資10萬元一年后的利潤.
(1)求X1,X2的概率分布和均值E(X1),E(X2);
(2)當E(X1)<E(X2)時,求p的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 是一個歷史文物展覽廳的俯視圖,點
是一個歷史文物展覽廳的俯視圖,點![]() 在
在![]() 上,在梯形
上,在梯形![]() 區域內部展示文物,
區域內部展示文物,![]() 是玻璃幕墻,游客只能在
是玻璃幕墻,游客只能在![]() 區域內參觀.在
區域內參觀.在![]() 上點
上點![]() 處安裝一可旋轉的監控攝像頭.
處安裝一可旋轉的監控攝像頭.![]() 為監控角,其中
為監控角,其中![]() 、
、![]() 在線段
在線段![]() (含端點)上,且點
(含端點)上,且點![]() 在點
在點![]() 的右下方.經測量得知:
的右下方.經測量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .記
.記![]() (弧度),監控攝像頭的可視區域
(弧度),監控攝像頭的可視區域![]() 的面積為
的面積為![]() 平方米.
平方米.

(1)求![]() 關于
關于![]() 的函數關系式,并寫出
的函數關系式,并寫出![]() 的取值范圍;(參考數據:
的取值范圍;(參考數據:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知雙曲線C: ![]() ﹣y2=1(a>0)的右焦點為F,點A,B分別在C的兩條漸近線AF⊥x軸,AB⊥OB,BF∥OA(O為坐標原點).
﹣y2=1(a>0)的右焦點為F,點A,B分別在C的兩條漸近線AF⊥x軸,AB⊥OB,BF∥OA(O為坐標原點). 
(1)求雙曲線C的方程;
(2)過C上一點P(x0 , y0)(y0≠0)的直線l: ![]() ﹣y0y=1與直線AF相交于點M,與直線x=
﹣y0y=1與直線AF相交于點M,與直線x= ![]() 相交于點N.證明:當點P在C上移動時,
相交于點N.證明:當點P在C上移動時, ![]() 恒為定值,并求此定值.
恒為定值,并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解一片經濟林的生長情況,隨機抽測了其中60株樹木的底部周長(單位:cm),所得數據均在區間[80,130]上,其頻率分布直方圖如圖所示,則在抽測的60株樹木中,有株樹木的底部周長小于100cm. 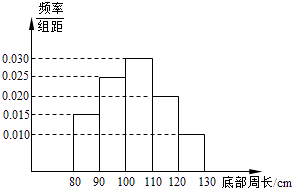
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為保護河上古橋OA,規劃建一座新橋BC,同時設立一個圓形保護區,規劃要求:新橋BC與河岸AB垂直;保護區的邊界為圓心M在線段OA上并與BC相切的圓,且古橋兩端O和A到該圓上任意一點的距離均不少于80m,經測量,點A位于點O正北方向60m處,點C位于點O正東方向170m處(OC為河岸),tan∠BCO= ![]() .
. 
(1)求新橋BC的長;
(2)當OM多長時,圓形保護區的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒中共有9個球,其中有4個紅球,3個黃球和2個綠球,這些球除顏色外完全相同.
(1)從盒中一次隨機取出2個球,求取出的2個球顏色相同的概率P;
(2)從盒中一次隨機取出4個球,其中紅球、黃球、綠球的個數分別記為x1 , x2 , x3 , 隨機變量X表示x1 , x2 , x3中的最大數,求X的概率分布和數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠在政府的幫扶下,準備轉型生產一種特殊機器,生產需要投入固定成本![]() 萬元,生產與銷售均已百臺計數,且每生產
萬元,生產與銷售均已百臺計數,且每生產![]() 臺,還需增加可變成本
臺,還需增加可變成本![]() 萬元,若市場對該產品的年需求量為
萬元,若市場對該產品的年需求量為![]() 臺,每生產
臺,每生產![]() 百臺的實際銷售收入近似滿足函數
百臺的實際銷售收入近似滿足函數![]() .
.
(![]() )試寫出第一年的銷售利潤
)試寫出第一年的銷售利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (單位:百臺,
(單位:百臺,![]() ,
,![]() )的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
)的函數關系式:(說明:銷售利潤=實際銷售收入-成本)
(![]() )因技術等原因,第一年的年生產量不能超過
)因技術等原因,第一年的年生產量不能超過![]() 臺,若第一年的年支出費用
臺,若第一年的年支出費用![]() (萬元)與年產量
(萬元)與年產量![]() (百臺)的關系滿足
(百臺)的關系滿足![]() ,問年產量
,問年產量![]() 為多少百臺時,工廠所得純利潤最大?
為多少百臺時,工廠所得純利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com