
【題目】已知函數f(x)=lg(mx2+mx+1),若此函數的定義域為R,則實數m的取值范圍是;若此函數的值域為R,則實數m的取值范圍是 .
【答案】[0,4);[4,+∞)
【解析】解:(1.)∵函數f(x)=lg(mx2+mx+1)的定義域為R,∴mx2+mx+1>0在R上恒成立,
①當m=0時,有1>0在R上恒成立,故符合條件;
②當m≠0時,由 ![]() ,
,
解得0<m<4,
綜上,實數m的取值范圍是[0,4).
(2.)令g(x)=mx2+mx+1的值域為A,
∵函數f(x)=lg(mx2+mx+1)的值域為R,
∴(0,+∞)A,
當m=0時,g(x)=1值域不是為R,不滿足條件;
當m≠0時, ![]() ,解得:m≥4,
,解得:m≥4,
所以答案是:[0,4),[4,+∞).
【考點精析】關于本題考查的函數的定義域及其求法,需要了解求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零才能得出正確答案.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為參數.
為參數.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)討論函數![]() 極值點的個數,并說明理由;
極值點的個數,并說明理由;
(3)若對任意![]() ,
, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的短軸長為
的短軸長為![]() ,右焦點為
,右焦點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上異于左、右頂點
上異于左、右頂點![]() 的一點.
的一點.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與直線
與直線![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,證明:點
,證明:點![]() 關于直線
關于直線![]() 的對稱點在直線
的對稱點在直線![]() 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生在開學季準備銷售一種文具套盒進行試創業,在一個開學季內,每售出![]() 盒該產品獲利潤
盒該產品獲利潤![]() 元;未售出的產品,每盒虧損
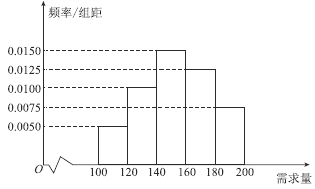
元;未售出的產品,每盒虧損![]() 元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示,該同學為這個開學季購進了
元.根據歷史資料,得到開學季市場需求量的頻率分布直方圖,如圖所示,該同學為這個開學季購進了![]() 盒該產品,以
盒該產品,以![]() (單位:盒,
(單位:盒, ![]() )表示這個開學季內的市場需求量,(單位:元)表示這個開學季內經銷該產品的利潤.
)表示這個開學季內的市場需求量,(單位:元)表示這個開學季內經銷該產品的利潤.
(1)根據直方圖估計這個開學季內市場需求量![]() 的中位數;
的中位數;
(2)將![]() 表示為
表示為![]() 的函數;
的函數;
(3)根據直方圖估計利潤不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一個分段函數可利用函數 ![]() 來表示,例如要表示一個分段函數
來表示,例如要表示一個分段函數 ![]() ,可將函數g(x)表示為g(x)=xS(x﹣2)+(﹣x)S(2﹣x).現有一個函數f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
,可將函數g(x)表示為g(x)=xS(x﹣2)+(﹣x)S(2﹣x).現有一個函數f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
(1)求函數f(x)在區間[0,4]上的最大值與最小值;
(2)若關于x的不等式f(x)≤kx對任意x∈[0,+∞)都成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x),若存在x∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點.已知函數f(x)=ax2+(b+1)x+(b﹣1)(a≠0).
(1)當a=1,b=2時,求函數f(x)的不動點;
(2)若對任意實數b,函數f(x)恒有兩個相異的不動點,求a的取值范圍;
(3)在(2)的條件下,若f(x)的兩個不動點為x1 , x2 , 且f(x1)+x2= ![]() ,求實數b的取值范圍.
,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為等腰梯形,
為等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 與
與![]() 相交于
相交于![]() ,且
,且![]() ,矩形
,矩形![]() 底面
底面![]() ,
,![]() 為線段
為線段![]() 上一動點,滿足
上一動點,滿足![]() .
.

(Ⅰ)若![]() 平面
平面![]() ,求實數
,求實數![]() 的值;
的值;
(Ⅱ)當![]() 時,銳二面角
時,銳二面角![]() 的余弦值為
的余弦值為![]() ,求多面體
,求多面體![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com