
分析 由f(x)=(2x-3)ex+$\frac{a}{x}$=0,可得a=x(3-2x)ex,令y=x(3-2x)ex,則y′=-(x-1)(2x+3)ex,取得函數的單調性,求出函數的極值,即可得出結論.
解答 解:由f(x)=(2x-3)ex+$\frac{a}{x}$=0,可得a=x(3-2x)ex,(x≠0)
令y=x(3-2x)ex,則y′=-(x-1)(2x+3)ex,
∴x<-$\frac{3}{2}$或x>1時,y′<0,函數單調遞減,-$\frac{3}{2}$<x<0或0<x<1時,y′>0,函數單調遞增,
∴x=-$\frac{3}{2}$時,函數取得極小值-9${e}^{-\frac{3}{2}}$,x=1時,函數取得極大值e,
∵f(x)=(2x-3)ex+$\frac{a}{x}$有三個零點,當x趨于負無窮的時候y是趨于零的
∴-9${e}^{-\frac{3}{2}}$<a<0,
故答案為-9${e}^{-\frac{3}{2}}$<a<0.
點評 本題考查函數的零點,考查導數知識的運用,考查學生分析解決問題的能力,正確分離變量是關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2017屆山東臨沭一中高三上學期10月月考數學(文)試卷(解析版) 題型:解答題
已知數列 是等差數列,
是等差數列, 是等比數列,且
是等比數列,且 ,
, ,
, .
.
(1)求數列 和
和 的通項公式;
的通項公式;
(2)數列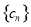 滿足
滿足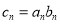 ,求數列
,求數列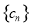 的前
的前 項和
項和
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com