已知

為

的內(nèi)角

的對邊,滿足
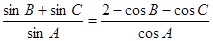
,函數(shù)


在區(qū)間

上單調(diào)遞增,在區(qū)間

上單調(diào)遞減.
(Ⅰ)證明:

;
(Ⅱ)若

,證明

為等邊三角形.
(1)根據(jù)正弦定理和兩角和差關(guān)系的運用來得到證明。
(2)根據(jù)余弦定理得到三邊長度相等來得到結(jié)論。
試題分析:解:(Ⅰ)根據(jù)題意,由于
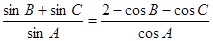
,根據(jù)正弦定理,可知

,
故可知

(Ⅱ)由題意知:由題意知:

,解得:

, 8分
因為

,
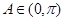
,所以

9分
由余弦定理知:

10分
所以
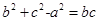
因為

,所以

,
即:

所以

11分
又

,所以

為等邊三角形. 12分
點評:主要是考查了解三角形的運用,屬于基礎(chǔ)題。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)

.
(Ⅰ)求函數(shù)

最大值和最小正周期;
(Ⅱ)設(shè)

的內(nèi)角

的對邊分別為

,且

,若

,求

的值
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
設(shè)θ為第二象限角,若tan(θ+

)=
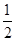
,則sinθ+cosθ=_________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在

△ABC中,

,則
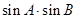
的最大值是_____________
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
在
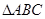
中,

為銳角,角

所對的邊分別為

,且

(Ⅰ)求

的值;
(Ⅱ)若

,求

的值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知

,
化簡:

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
在

中,角

的對邊
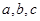
滿足:

,給出下列不等式:
①

;②

;③

.
其中一定成立的是 ( )
查看答案和解析>>

 為
為 的內(nèi)角
的內(nèi)角 的對邊,滿足
的對邊,滿足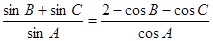 ,函數(shù)
,函數(shù)
 在區(qū)間
在區(qū)間 上單調(diào)遞增,在區(qū)間
上單調(diào)遞增,在區(qū)間 上單調(diào)遞減.
上單調(diào)遞減. ;
; ,證明
,證明 為等邊三角形.
為等邊三角形. .
. 最大值和最小正周期;
最大值和最小正周期; 的內(nèi)角
的內(nèi)角 的對邊分別為
的對邊分別為 ,且
,且 ,若
,若 ,求
,求 的值
的值